
PERIMETERS AND AREAS
Perimeters of Triangles and Quadrilaterals
The Perimeters of Triangles and Quadrilaterals
Find the perimeters of triangles and quadrilaterals
Perimeter – is defined as the total length of a closed shape. It is obtained by adding the lengths of the sides inclosing the shape. Perimeter can be measured in 𝑚𝑚 , 𝑐𝑚 ,𝑑𝑚 ,𝑚,𝑘𝑚 e. t. c
Examples
Example 1
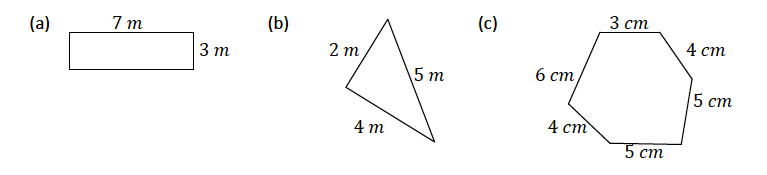
Find the perimeters of the following shapes
Solution
- Perimeter = 7𝑚 + 7𝑚 + 3𝑚 + 3𝑚 = 20 𝑚
- Perimeter = 2𝑚 + 4𝑚 + 5𝑚 = 11 𝑚
- Perimeter = 3𝑐𝑚 + 6𝑐𝑚 + 4𝑐𝑚 + 5𝑐𝑚 + 5 𝑐𝑚 + 4𝑐𝑚 = 27 𝑐𝑚
Circumference of a Circle
The Value of Pi ( Π)
Estimate the value of Pi ( Π)
The number π is a mathematical constant, the ratio of a circle's circumference to its diameter, commonly approximated as3.14159. It has been represented by the Greek letter "π" since the mid 18th century, though it is also sometimes spelled out as "pi" (/paɪ/).
The perimeter of a circle is the length of its circumference 𝑖. 𝑒 𝑝𝑒𝑟𝑖𝑚𝑒𝑡𝑒𝑟 = 𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒. Experiments show that the ratio of the circumference to the diameter is the same for all circles

The Circumference of a Circle
Calculate the circumference of a circle
Example 2
Find the circumferences of the circles with the following measurements. Take 𝜋 = 3.14
- diameter 9 𝑐𝑚
- radius 3½𝑚
- diameter 4.5 𝑑𝑚
- radius 8 𝑘𝑚
Solution
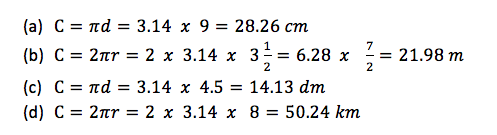
Example 3
The circumference of a car wheel is 150 𝑐𝑚. What is the radius of the wheel?
Solution
Given circumference, 𝐶 = 150 𝑐𝑚
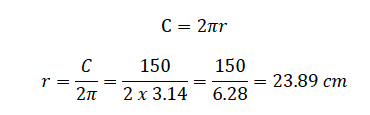
∴ The radius of the wheel is 23.89 𝑐𝑚
Areas of Rectangles and Triangles
The Area of a Rectangle
Calculate the area of a rectangle
Area – can be defined as the total surface covered by a shape. The shape can be rectangle, square, trapezium e. t. c. Area is measured in mm!, cm!,dm!,m! e. t. c
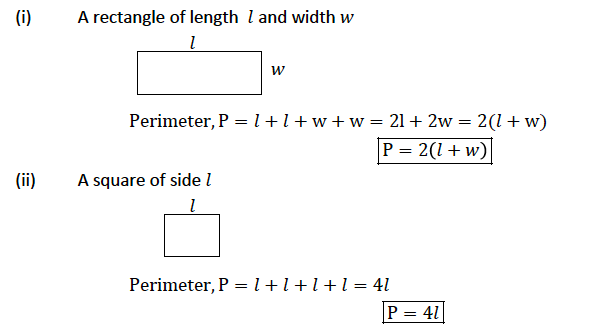
Consider a rectangle of length 𝑙 and width 𝑤
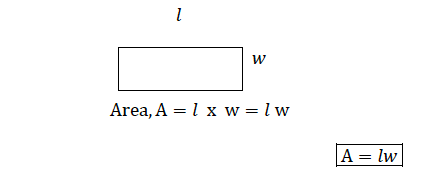
Consider a square of side 𝑙
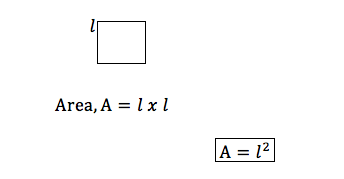
Consider a triangle with a height, ℎ and a base, 𝑏
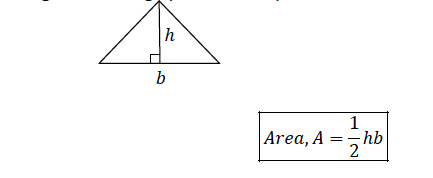
Areas of Trapezium and Parallelogram
The Area of a Parallelogram
Calculate area of a parallelogram
A parallelogram consists of two triangles inside. Consider the figure below:
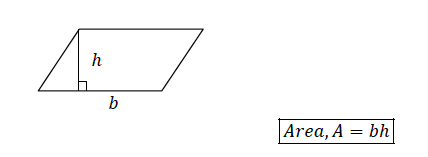
The Area of a Trapezium
Calculate the area of a trapezium
Consider a trapezium of height, ℎ and parallel sides 𝑎 and 𝑏
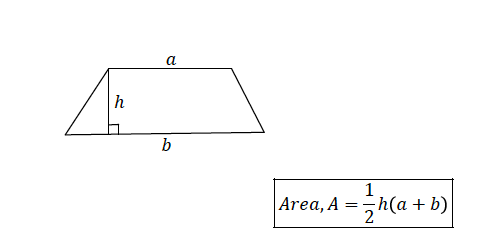
Example 4
The area of a trapezium is120 𝑚!. Its height is 10 𝑚 and one of the parallel sides is 4 𝑚. What is the other parallel side?
Solution
Given area, 𝐴 = 120 𝑚2, height, ℎ = 10 𝑚, one parallel side, 𝑎 = 4 𝑚. Let other parallel side be, 𝑏
Then

Area of a Circle
Areas of Circle
Calculate areas of circle
Consider a circle of radius r;
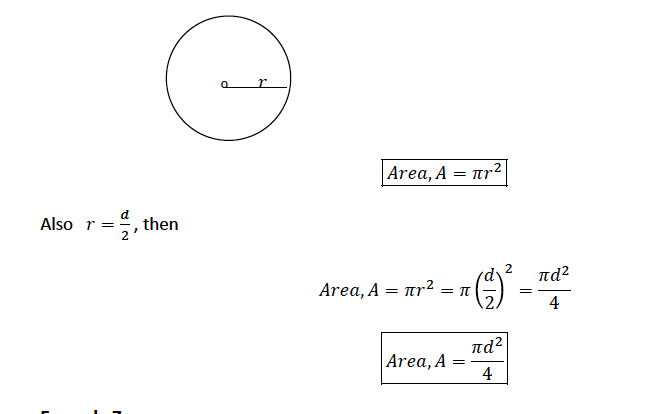
Example 5
Find the areas of the following figures
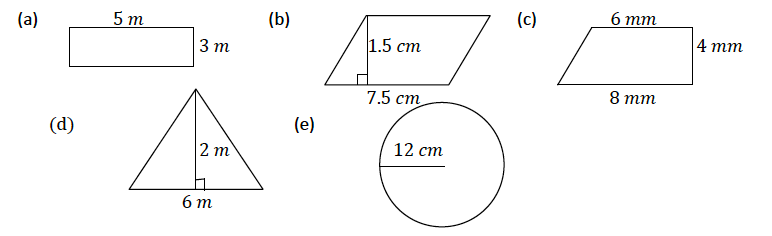
Solution
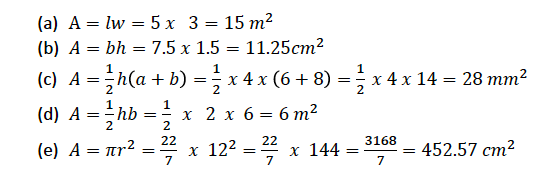
Example 6
A circle has a circumference of 30 𝑚. What is its area?
Solution
Given circumference, 𝐶 = 30 𝑚
C = 2𝜋𝑟
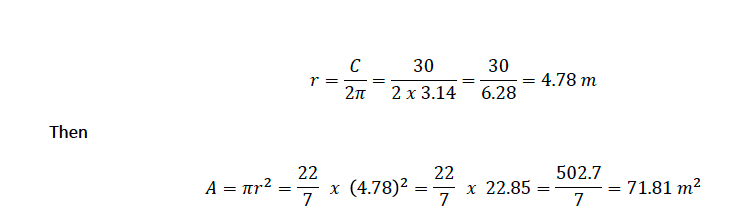



No comments:
Post a Comment