
RATIO, PROFIT AND LOSS
Ratio
A ratio – is a way of comparing quantities measured in the same units
Examples of ratios
- A class has 45 girls and 40 boys. The ratio of number of boys to the number of girls = 40: 45
- A football ground 100 𝑚 long and 50 𝑚 wide. The ratio of length to the width = 100: 50
NOTE: Ratios can be simplified like fractions
- 40: 45 = 8: 9
- 100: 50 = 2: 1
A Ratio in its Simplest Form
Express a ratio in its simplest form
Example 1
Simplify the following ratios, giving answers as whole numbers

Solution

A Given Quantity into Proportional Parts
Divide a given quantity into proportional parts
Example 2
Express the following ratios in the form of

Solution

To increase or decrease a certain quantity in a given ratio, multiply the quantity with that ratio
Example 3
- Increase 6 𝑚 in the ratio 4 ∶ 3
- Decrease 800 /− in the ratio 4 ∶ 5
Solution

Profits and Loss
Profit or Loss
Find profit or loss
If you buy something and then sell it at a higher price, then you have a profit which is given by: Profit = selling price − buying price
If you buy something and then sell it at a lower price, then you have a loss which is given by: Loss = buying price − selling price
The profit or loss can also be expressed as a percentage of buying price as follows:
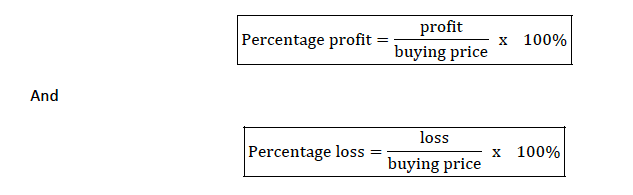
Percentage Profit and Percentage Loss
Calculate percentage profit and percentage profit and percentage loss
Example 4
Mr. Richard bought a car for 3, 000, 000/− and sold for 3, 500, 000/−. What is the profit and percentage profit obtained?
Solution
Profit= selling price − buying price = 3,500,000-3,000,000=500,000
Therefore the profit obtained is 500,000/-
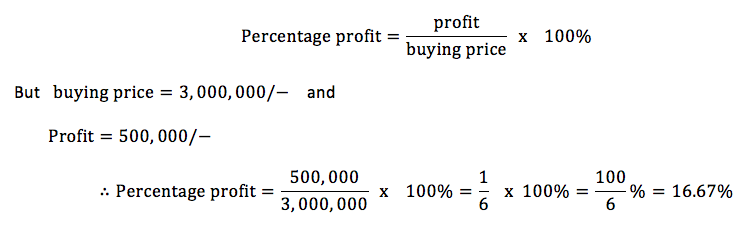
Example 5
Eradia bought a laptop for
Solution

But buying price = 780, 000/− and loss = buying price − selling price = 780, 000 − 720, 000 = 60, 000/−
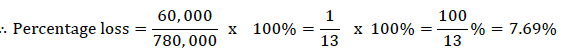
Simple Interest
Simple Interest
Calculate simple interest
The amount of money charged when a person borrows money e. g from a bank is called interest (I)
The amount of money borrowed is called principle (P)
To calculate interest, we use interest rate (R) given as a percentage and is usually taken per year or per annum (p.a)
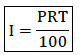
Example 6
Calculate the simple interest charged on the following
- 850, 000/− at 15% per annum for 9 months
- 200, 000/− at 8% per annum for 2 years
Solution
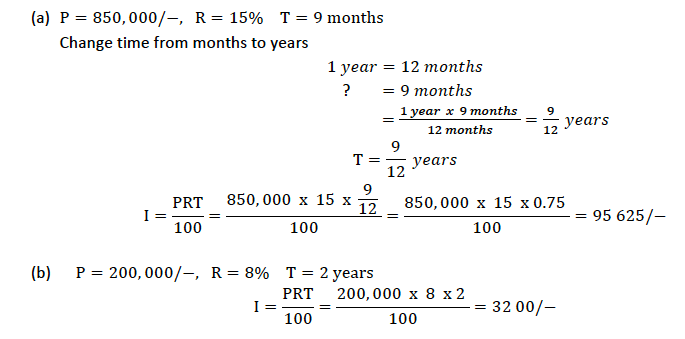
Real Life Problems Related to Simple Interest
Solve real life problems related to simple interest
Example 7
Mrs. Mihambo deposited money in CRDB bank for 3 years and 4 months. A t the end of this time she earned a simple interest of 87, 750/− at 4.5% per annum. How much had she deposited in the bank?
Solution
Given I = 87, 750/− R = 4.5% % T = 3 years and 4 months
Change months to years
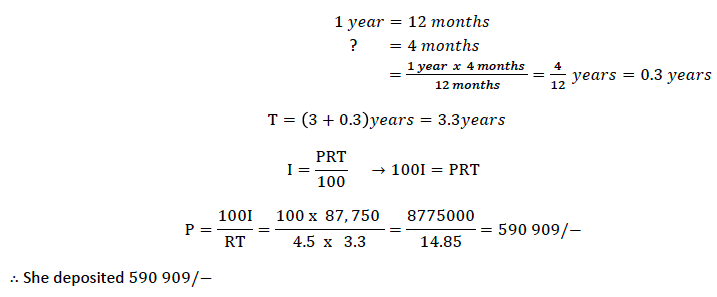
- READ TOPIC 10: Coordinate Geometry



No comments:
Post a Comment