
STATISTICS
Mean
Calculating the Mean from a Set of Data, Frequency Distribution Tables and Histogram
Calculate the mean from a set of data, frequency distribution tables and histogram
Measures of central tendency:
After collecting the data, organizing it and illustrating it by means of diagrams, there is a need to calculate certain statistical measures to describe the data more precisely. There are various types of measures of central tendency – the arithmetic mean (or simply the mean), the median, and the mode. Once the measures of central tendency are found, it is easier to compare two or more sets of data.
The arithmetic mean
When people are asked to find the measure of central tendency of some numbers, they usually find the total of the numbers, and then divide this total by however many numbers there are. This type of measure of central tendency is the arithmetic mean. If the n values are x1+x2+x3 ………+xn then the arithmetic mean is = x1 + x2+ ….. + xn/n

Example 1
The masses of some parcels are 5kg, 8kg, 20kg and 15kg. Find the mean mass of the parcels.
Solution
Total mass = (5 + 8 + 20 + 15) kg = 48kg
The number of parcels = 4
The mean mass = 48kg ÷ 4 = 12kg
The arithmetic mean used as measure of central tendency can be misleading as can be seen in the following example.
Example 2
John and Mussa played for the local cricket team. In the last six batting innings, they scored the following number of runs.John: 64, 0, 1, 2, 4, 1;Mussa: 15, 20, 13, 11 , 10, 3.Find the mean score of each player. Which player would you rather have in your team? Give a reason.
Solution
John’s mean = (64 + 0 + 1 + 2 + 4 + 1) ÷ 6 = 12
Mussa’s mean = (15 + 20 + 13 + 11 + 10 + 3) ÷ 6 = 12
Each player has the same mean score. However, observing the individual scores suggests that they are different types of player. If you are looking for a steady reliable player, you would probably choose Mussa.
Often it is possible to use the mean of one set of numbers to find the mean of another set of related numbers.
Suppose a number a is added to or subtracted from all the data. Then a is added to or subtracted from the mean.
Suppose the n values are 𝑥!+𝑥! + 𝑥! .........+𝑥!. Multiply each by a, and we obtain 𝑎𝑥!+𝑎𝑥! + 𝑎𝑥! .........+𝑎𝑥!. So we see that the mean has been multiplied by a.
Interpreting the Mean Obtained from a Set Data, Frequency Distribution Tables and Histogram
Interpret the mean obtained from a set data, frequency distribution tables and histogram
Measures of central tendency from frequency tables
If the data has already been put into a frequency table, the calculation of the measures of central tendency is slightly easier.
Exercise 1
Juma rolled a six- sided die 50 times. The scores he obtained are summarized in the following table.Calculate the mean score
| Score (x) | 1 | 2 | 3 | 4 | 5 | 6 |
| Frequency (f) | 8 | 10 | 7 | 5 | 12 | 8 |
Solution
10 scores of 2 give a total 10 x 2 = 20
8 scores of 1 gives a total 8 x 1 = 8
And so on, giving a total score of
8 x 1 +10 x 2+7 x 3 + 5 x 4 + 12 x 5 + 8 x 6 = 177
The total frequency = 8 + 10 + 7 + 5 + 12 + 8 = 50
Medium
The Concept of Median
Explain the concept of median
Mr.Samwel owns a small factory. He earns about 4,000,000/- from it each year. He employs 4 people. They earn 550,000/-, 500,000/-, 450,000/- and 400, 000/-.The mean income of these five people is(4,000,000 + 550,000 + 500,000 + 450,000 + 400,000 ÷ 5 = 1,180,000/-
If you said to one the employees that they earned about 1,180,000/- each year they would disagree with you. In this type of situation when one of the values is different from the others (as in Example 2), the mean is not the best measure of central tendency to use.Arrange the incomes in increasing order of size as follows:
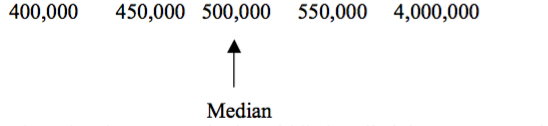
The value that appears in the middle is called the median. In this case the value of 500,000/- is a much better idea of the average wage earned by the employees. The median is not affected by isolated values (sometimes called rogue values) that are much larger or smaller than the rest of the data.
If the data consists of an even number of values, find the mean of two middle values as shown in the next example.
The Medium from a Set of Data
Calculate the medium from a set of data
Example 3
Find the median of the numbers: 12, 23, 10, 8, 22, 14, 30, and 18.
Solution
Arranging in increasing order of size, we get 8 10 12 14 18 22 23 30
Median = (14 + 18) ÷ = 16
The Median using Frequency Distribution Tables and Cumulative Curve
Find the median using frequency distribution tables and cumulative curve
Example 4
Juma rolled a six- sided die 50 times. The scores he obtained are summarized in the following table. Calculate the modianl score
Solution
here are 50 items of data, so if you arrange them in order of size, the positions are1 .................... 25 and 26 ................. 50. The median will be the average of the 25th and 26th number.
In the table there are 8 scores of 1, followed by 10 scores of 2. This gives you 8 + 10 = 18 numbers. These are then followed by 7 scores of 3. This gives 18 + 7 = 25 numbers. It follows that the 25th number is a 3. The 26th number must be the first number in the next group, which is a 4.
The median is then = (3 + 4) ÷ 2 = 3.5
The Median Obtained from the Data
Interpret the median obtained from the data
Exercise 2
- The times of five athletes in the 100 m were: 12.5 s, 12.9s, 14.8s, 15.0s, 25.2s. Find the median time. Why is the median a better measure of central tendency to use than the mean?
- Iddi has 6 maths tests during a school term. His marks are recorded below. Find the mean and the median mark. Explain why the median is a better measure of central tendency than the mean 73 78 82 0 75 86
- The table below gives the percentage prevalence of HIV infection in female blood donors for the years 1992 to 2003. Find the mean and median of these figures.
| 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| 5.9 | 6.2 | 4.8 | 9.4 | 8.2 | 11.6 | 11.8 | 12.6 | 13.3 | 13.7 | 12.3 | 11.9 |
Mode
The Concept of Mode
Explain the concept of mode
The mode is value that occurs most often in a set of data.This is another measure of central tendency. It is possible for data to have more than one mode.
Data with two modes are said to be bi – modal.Why mode? The mode is often important to know. For example:
- If you ran a shoe shop you would want to know the most popular size.
- If you ran a restaurant you would want to know what type of food is ordered most.
The Mode
Calculate the mode
Example 5
State the mode for the following sets of numbers:
- 0, 0, 1, 1, 1, 2, 2, 3, 4, 5, 5
- 58, 57, 60, 59, 50, 56, 62
- 5, 10, 10, 10, 15, 15, 20, 20, 20, 25
Solution
- 1 occurs most (3 times): The mode is 1
- All the numbers appear once: There is no mode.
- There are three 10s and three 20s: Modes are 10 and 20.
Exercise 3
- Ten pupils were asked how many brothers or sisters they had. The results are recorded below. Find the mode number 0, 1 , 1, 2, 5, 0, 1 3 , 1 and 4.
- Eight motorists were asked how many times they had taken the driving test before they passed. The results are recorded below. Find the mode number. 14213141
- Give examples of where the mode is a better measure of central tendency than either the mean or the median.
- Find the mode of these sets of numbers.
- 0, 1, 1, 3, 4, 5, 5, 5, 6, 7, 8
- 3, 8, 4, 3, 8, 4, 3, 8, 8, 3, 3, 4
- 5, 12, 6, 5, 11, 12, 5, 5, 8, 12, 7, 12
- 3, 6, 2, 8, 2, 1, 9, 12, 15
Finding the Mode using Frequency Distribution and a Histogram
Find the mode using frequency distribution and a histogram
Grouped data
Suppose a set of data consists of many different values, such as heights of people measured to the nearest centimeter. Then the data is grouped, for example into 160 – 165 cm, and so on. If the data has been grouped together in classes, then unless you have a list of all the individual values, you only know approximately what each value is. For this reason, you can only estimate the mean and the median. Also, if all the values are different, you do not have a single value as the mode. Instead you have a modal class, as shown in the example below.
Data grouped in classes can be illustrated by a histogram.Suppose one of the intervals is from 10 to 19, where data has been rounded to the nearest whole number. The class limits are 10 and 19. The data in this interval could be as low as 9.5 or as high as 19.5. These are the class boundaries. The width of the interval is the difference between the class boundaries, in this case it is 10.
The histogram consists of rectangles between the class boundaries, with height corresponding to the frequency. The area of each rectangle is proportional to the frequency.
Example 6
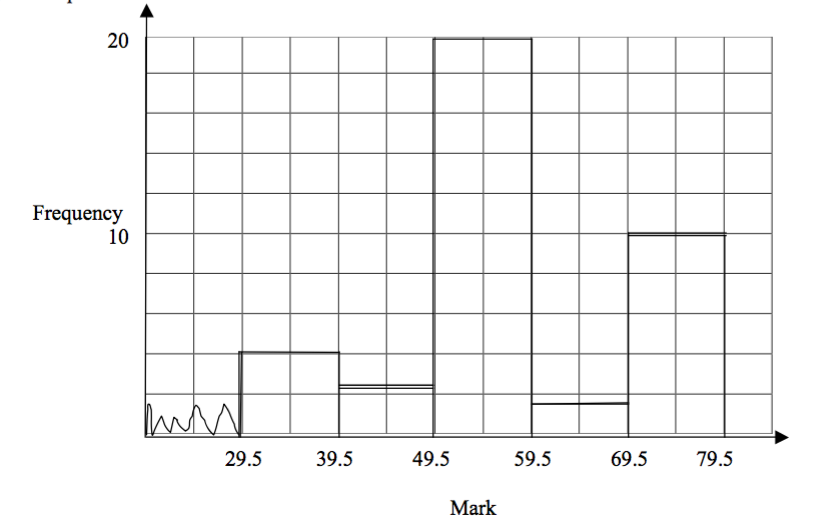
The examination results (rounded to the nearest whole number %) are given for a group of students.
| Mark (%) | 30 – 39 | 40 -49 | 50 – 59 | 60 - 69 | 70 - 79 |
| Frequency | 5 | 3 | 20 | 2 | 10 |
- Draw a histogram
- state the modal class
Solution
For a histogram, the horizontal axis is for the data values, and the vertical axis is for the frequencies. So label the horizontal axis with the marks from 30 to 80. To indicate that the axis does not start at 0 put a zig – zag to the left of 30. Label the vertical axis with frequencies from 0 to 20. The first interval has limits 30 and 39. The class boundaries are 29.5 and 39.5. It has a frequency of 5. So draw a box covering the interval, and with height 5. Repeat with the other intervals
Interpreting the Mode Obtained from the Data
Interpret the mode obtained from the data
Example 7
The examination results (rounded to the nearest whole number %) are given for a group of students.
| Mark (%) | 30 – 39 | 40 -49 | 50 – 59 | 60 - 69 | 70 - 79 |
| Frequency | 5 | 3 | 20 | 2 | 10 |
Estimate the mode
Solution
To estimate the mode, there are two methods.
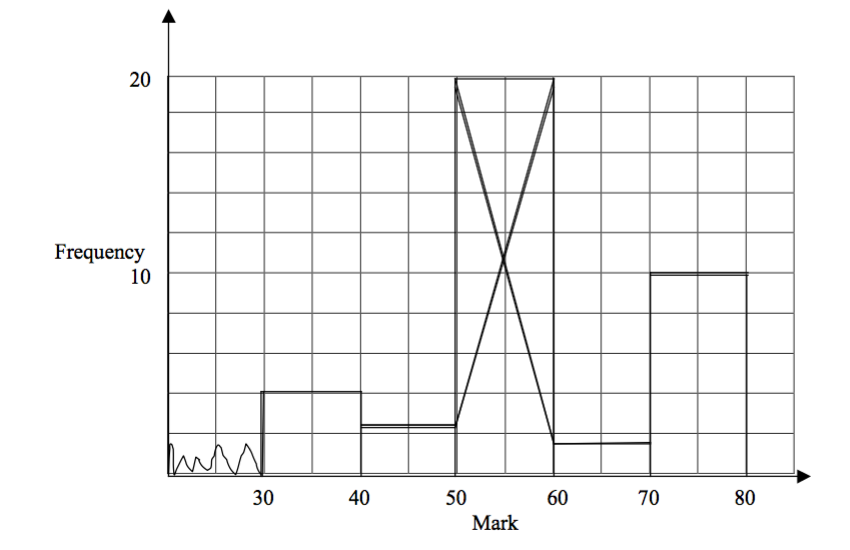
By drawing:Use the histogram of the first part.Then proceed as follow;
- Step 1: Draw a straight line from the top left hand corner of the rectangle of the modal class, to the top left hand corner of the rectangle of the class to the right of the modal class.
- Step 2: Draw a line from the top right hand corner of the rectangle of the modal class,to the top right of the modal class to the left of the modal class.
- Step 3: Find where these two lines intersect. This gives the mode as 54 on the horizontal axis.
By calculation:Let
- fM = frequency of the modal group
- fR = frequency of the group to the right of the modal group
- fL = frequency of the group to the left of the modal group
- W = width of the modal group
- L = lower class boundary of the modal group
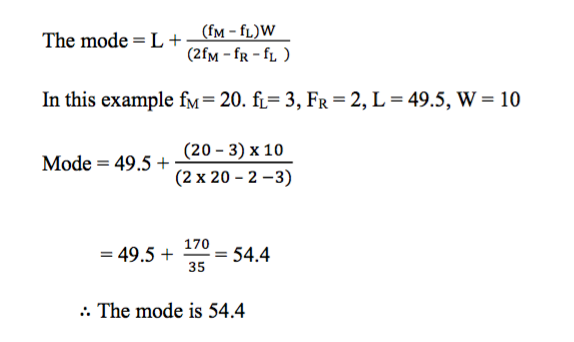
- READ TOPIC 4: Rates And Variations



No comments:
Post a Comment