
CIRCLES
Definition of Terms
Circle, Chord, Radius, Diameter, Circumference, Arc, Sector, Centre and Segment of a Circle
Define circle, chord, radius, diameter, circumference, arc, sector, centre and segment of a circle
A circle: is the locus or the set of all points equidistant from a fixed point called the center.
Arc: a curved line that is part of the circumference of a circle
Chord: a line segment within a circle that touches 2 points on the circle.
Circumference: The distance around the circle.
Diameter: The longest distance from one end of a circle to the other.
Origin: the center of the circle
Pi(π):A number, 3.141592..., equal to (the circumference) / (the diameter) of any circle.
Radius: distance from center of circle to any point on it.
Sector: is like a slice of pie (a circle wedge).
Tangent of circle: a line perpendicular to the radius that touches ONLY one point on the circle.
NB: Diameter = 2 x radius of circle
Circumference of Circle = PI x diameter = 2 PI x radius
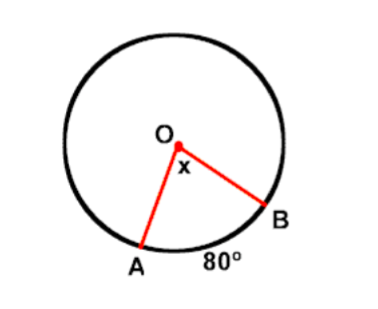
Central Angle
The Formula for the Length of an Arc
Derive the formula for the length of an arc
Circumference of Circle = PI x diameter = 2 PI x radius where PI =𝝅= 3.141592...
The Central Angle
Calculate the central angle
A central angle is an angle formed by two intersecting radii such that its vertex is at thecenter of the circle.

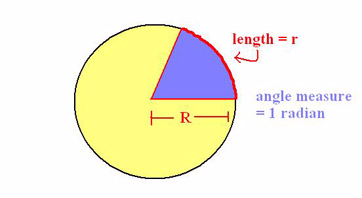
The Concept of Radian Measure
Explain the concept of radian measure
Radians are the standard mathematical way to measure angles. One radian is equal to the angle created by taking the radius of a circle and stretching it along the edge of the circle.
The radian is a pure mathematical measurement and therefore is preferred by mathematicians over degree measures. For use in everyday work, the degree is easier to work with, but for purely mathematical pursuits, the radian gives better results. You probably will never see radian measures used in construction or surveying, but it is a common unit in mathematics and physics.
Radians to Degree and Vice Versa
Convert radians to degree and vice versa
The unit used to describe the measurement of an angle that is most familiar is thedegree. To convert radians to degrees or degrees to radians, the following relationship can be used.
angle in degrees = angle in radians * (180/pi)
So, 180 degrees = pi radians
Example 1
Convert 45 degrees to radians
Solution
45 = 57.32*radians
radians = 45/57.32
radians = 0.785
Most often when writing degree measure in radians, pi is not calculated in, so for this problem, the more accurate answer would beradians = 45 pi/180 = pi/4
Example 2
Convert pi/3 radians to degree
degrees = (pi/3) * (180/pi)
degrees = 180/3 = 60°
Angles Properties
Circle Theorems of Inscribed Angles
Prove circle theorems of inscribed angles
Aninscribedangle is formed when two secant lines intersect on a circle. It can also be formed using a secant line and a tangent line intersecting on a circle. Acentral angle, on the other hand, is an angle whose vertex is the center of the circle and whose sides pass through a pair of points on the circle, therefore subtending an arc.In this post, we explore the relationship between inscribed angles and central angles having the same subtended arc. The angle of the subtended arc is the same as the measure of the central angle (by definition).
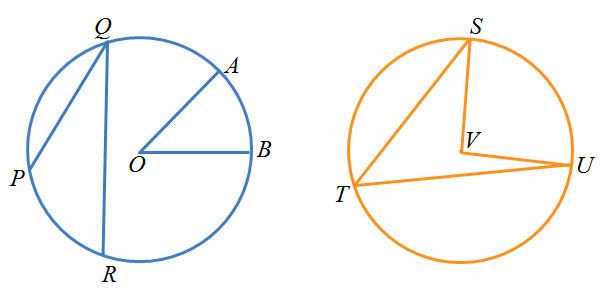
In the first circle,is a central angle subtended by arc. Angleis an inscribed angle subtended by arc. In the second circle,is an inscribed angle andis a central angle. Both angles are subtending arc.
What can you say about the two angles subtending the same arc? Draw several cases of central angles and inscribed angles subtending the same arc and measure them. Use a dynamic geometry software if necessary. Are your observations the same?
In the discussion below, we prove one of the three cases of the relationship between a central angle and an inscribed angle subtending the same arc.
Theorem
The measure of an angle inscribed in a circle is half the measure of the arc it intercepts. Note that this is equivalent to the measure of the inscribed angle is half the measure of the central angle if they intercept the same arc.
Proof
Letbe an inscribed angle andbe a central angle both subtending arcas shown in the figure. Draw line. This forms two isosceles trianglesandsince two of their sides are radii of the circle.
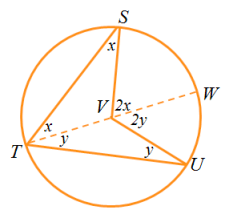
In triangle, if we let the measure ofbe, then angleis also. By theexterior angle theorem, the measure of angle. This is also similar to triangle. If we let angle, it follows thatis equal to 2y. In effect, the measure of the inscribed angleand the measure of central anglewhich is what we want to prove.
The Circle Theorems in Solving Related Problems
Apply the circle theorems in solving related problems
Example 3
An arc subtends an angle of 200 at the center of the circle of radius25cm.Find the length of this arc.
Solution
r =25cm, 𝜽=20°
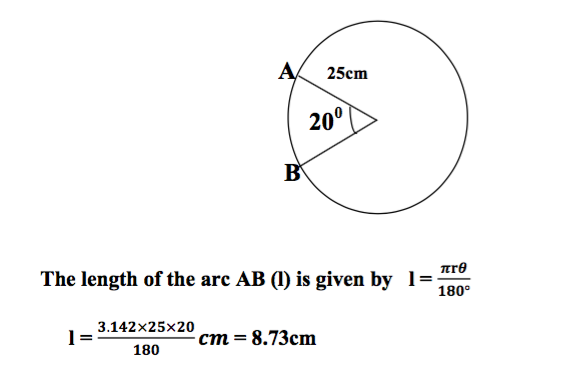
The length of the arc is 8.73cm.
Example 4
An arc of length 5cm subtends 50° at the center of the circle, what is theradius of the circle?
l=5cm, 𝜽=50°, r=?
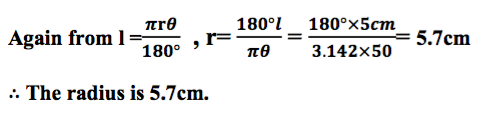
Chord Properties of a Circle
Chord Properties of a Circle
Identify chord properties of a circle
Imagine that you are on one side of a perfectly circular lake and looking across to a fishing pier on the other side. The chord is the line going across the circle from point A (you) to point B (the fishing pier). The circle outlining the lake's perimeter is called thecircumference. Achord of a circleis a line that connects two points on a circle's circumference.
To illustrate further, let's look at several points of reference on the same circular lake from before. If each point of reference (i.e. duck feeding area, picnic tables, you, water fountain, and fishing pier) were directly on this lake's circumference, then each line connecting a point to another point on the circle would be chords.
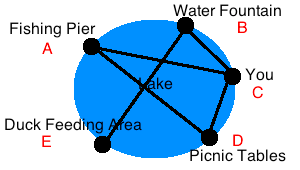
- The line between the fishing pier and you is now chord AC
- The line between the water fountain and duck feeding area is now chord BE
- The line between you and the picnic tables is chord CD
If we had a chord that went directly through the center of a circle, it would be called adiameter. If we had a line that did not stop at the circle's circumference and instead extended into infinity, it would no longer be a chord; it would be called asecant.
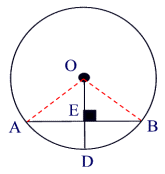
The Theorem on the Perpendicular Bisector to a Chord
Prove the theorem on the perpendicular bisector to a chord.
Proof of Theorem
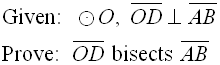
The Theorem on Parallel Chords
Prove the theorem on parallel chords
Parallel chords in the same circle always cut congruent arcs. Parallel chords intercept congruent arcs.
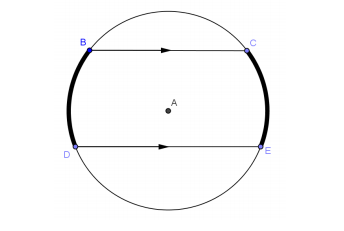
- Construct a diameter perpendicular to the parallel chords.
- What does this diameter do to each chord? The diameter bisects each chord.
- Reflect across the diameter (or fold on the diameter). What happens to the endpoints?The reflection takes the endpoints on one side to the endpoints on the other side. It, therefore, takes arc to arc. Distances from the center are preserved.
- What have we proven? Arcs between parallel chords are congruent.
The Theorems on Chords in Solving Related Problems
Apply the theorems on chords in solving related problems
Example 5
The figure is a circle with centre O. Given PQ= 12 cm. Find the length of PA.
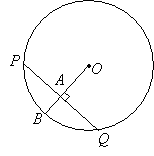
Solution:
The radius OB is perpendicular to PQ. So,OB is a perpendicular bisector of PQ.
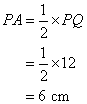
Example 6
The figure is a circle with centre O and diameter 10 cm.PQ= 1 cm. Find the length of RS.
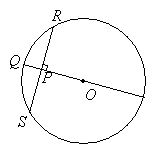
Solution:
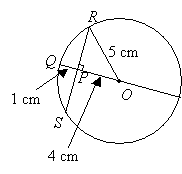

Tangent Properties
A Tangent to a Circle
Describe a tangent to a circle
Tangent is a line which touches a circle. The point where the line touches the circle is called the point of contact. A tangent is perpendicular to the radius at the point of contact.
Tangent Properties of a Circle
Identify tangent properties of a circle
A tangent to a circle is perpendicular to the radius at the point of tangency. A common tangent is a line that is a tangent to each of two circles. A common external tangent does not intersect the segment that joins the centers of the circles. A common internal tangent intersects the segment that joins the centers of the circles.
Tangent Theorems
Prove tangent theorems
Theorem 1
If two chords intersect in a circle, the product of the lengths of the segments of one chord equal the product of the segments of the other.
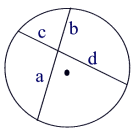
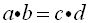
Intersecting Chords Rule: (segment piece)×(segment piece) =(segment piece)×(segment piece)
Theorem Proof:
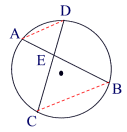
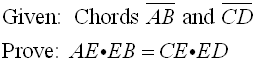
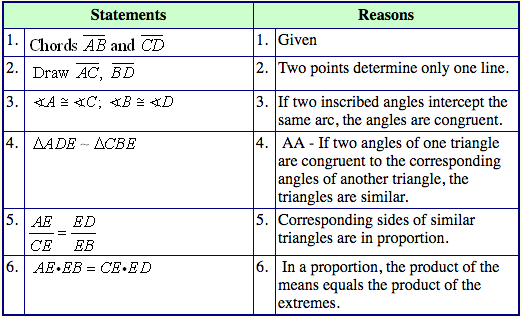
Theorem 2:
If two secant segments are drawn to a circle from the same external point, the product of the length of one secant segment and its external part is equal to the product of the length of the other secant segment and its external part.
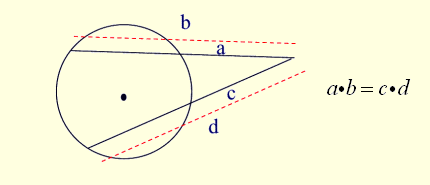
Secant-Secant Rule: (whole secant)×(external part) =(whole secant)×(external part)
Theorem 3:
If a secant segment and tangent segment are drawn to a circle from the same external point, the product of the length of the secant segment and its external part equals the square of the length of the tangent segment.
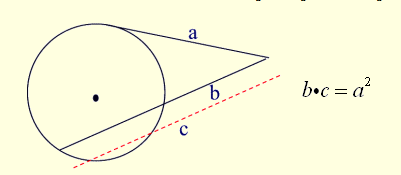
Secant-Tangent Rule:(whole secant)×(external part) =(tangent)2
Theorems Relating to Tangent to a Circle in Solving Problems
Apply theorems relating to tangent to a circle in solving problems
Example 7
Two common tangents to a circle form a minor arc with a central angle of 140 degrees. Find the angle formed between the tangents.
Solution
Two tangents and two radii form a figure with 360°. If y is the angle formed between the tangents then y + 2(90) + 140° = 360°
y = 40°.
The angle formed between tangents is 40 degrees.
- READ TOPIC 7: The Earth As A Sphere



No comments:
Post a Comment