MATHEMATICS FORM FOUR TOPIC 1: COORDINATE GEOMETRY

COORDINATE GEOMETRY

Equation of a Line

The General Equation of a Straight Line

Derive the general equation of a straight line

COORDINATES OF A POINT

•The coordinates of a points - are the values of x and y enclosed by the brackets which are used to describe the position of point in a line in the plane.

The plane is called xy-plane and it has two axis.

1. horizontal axis known as axis and
2. vertical axis known as axis

Consider the xy-plane below

The coordinates of points A, B, C ,D and E are A(2, 3), B(4, 4), C(-3, -1), D(2, -4) and E(1, 0).

Definition

Example 1

Find the gradient of the lines joining

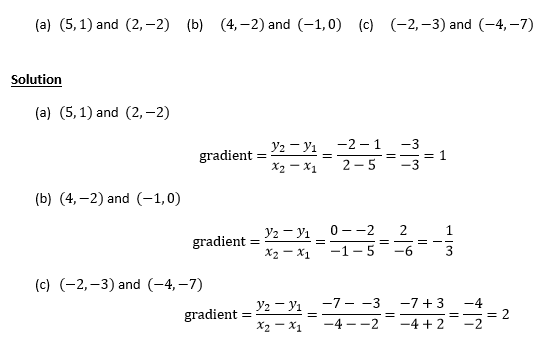
Example 2

(a) The line joining (2, -3) and (k, 5) has a gradient -2. Find k

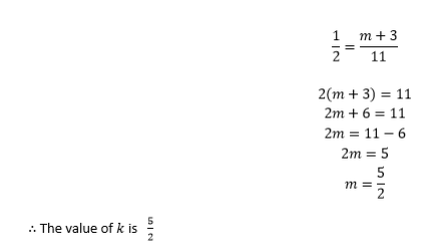
Exercise 1

1. Find the gradientof the line which passes through the following points ;

1. (3,6) and (-2,8)
2. (0,6) and (99,-12)
3. (4,5)and (5,4)

2. A line passes through (3, a) and (4, -2), what is the value of a if the slope of the line is 4?

3. The gradient of the linewhich goes through (4,3) and (-5,k) is 2. Find the value of k.

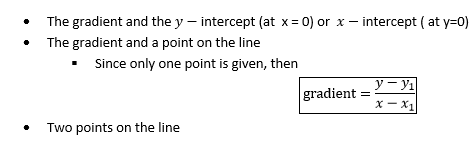
FINDING THE EQUATION OF A STRAIGHT LINE

The equation of a straight line can be determined if one of the following is given:-

Example 3

Find the equation of the line with the following

1. Gradient 2 and intercept
2. Gradient and passing through the point
3. Passing through the points and

Solution

EQUATION OF A STRAIGHT LINE IN DIFFERENT FORMS

The equation of a line can be expressed in two forms

Example 4

Find the gradient of the following lines

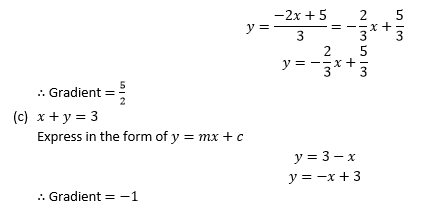
INTERCEPTS

Therefore

Example 5

Find the y-intercept of the following lines

Example 6

Find the x and y-intercept of the following lines

Exercise 2

Attempt the following Questions.

1. Find the y-intercept of the line 3x+2y = 18 .
2. What is the x-intercept of the line passing through (3,3) and (-4,9)?
3. Calculate the slope of the line given by the equation x-3y= 9
4. Find the equation of the straight line with a slope -4 and passing through the point (0,0).
5. Find the equation of the straight line with y-intercept 5 and passing through the point (-4,8).

GRAPHS OF STRAIGHT LINES

The graph of straight line can be drawn by using the following methods;

1. By using intercepts
2. By using the table of values

Example 7

Sketch the graph of Y = 2X - 1

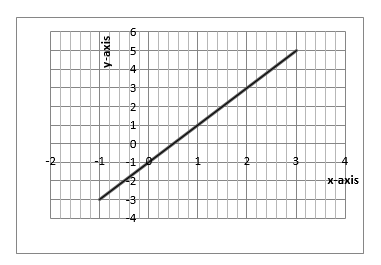
SOLVING SIMULTANEOUS EQUATION BY GRAPHICAL METHOD

• Use the intercepts to plot the straight lines of the simultaneous equations
• The point where the two lines cross each other is the solution to the simultaneous equations

Example 8

Solve the following simultaneous equations by graphical method

Exercise 3

1. Draw the line 4x-2y=7 and 3x+y=7 on the same axis and hence determine their intersection point

2. Find the solutionfor each pair the following simultaneous equations by graphical method;

1. y-x = 3 and 2x+y = 9
2. 3x- 4y=-1 and x+y = 2
3. x = 8 and 2x-3y = 10

Midpoint of a Line Segment

The Coordinates of the Midpoint of a Line Segment

Determine the coordinates of the midpoint of a line segment

Let S be a point with coordinates (x₁,y₁), T with coordinates (x₂,y₂) and M with coordinates (x,y) where M is the mid-point of ST. Consider the figure below:

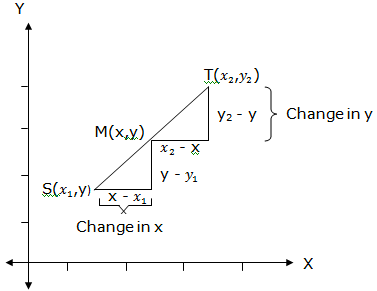
Considering the angles of the triangles SMC and TMD, the triangles SMC and TMD are similar since their equiangular

Example 9

Find the coordinates of the mid-point joining the points (-2,8) and (-4,-2)

Solution

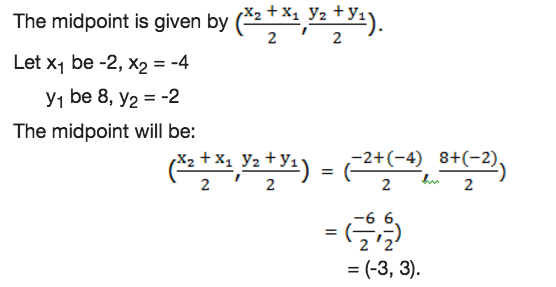
Therefore the coordinates of the midpoint of the line joining the points (-2,8) and (-4, -2) is (-3,3).

Distance Between Two Points on a Plane

The Distance Between Two Points on a Plane

Calculate the distance between two points on a plane

Consider two points, A(x₁,y₁) and B(x₂,y₂) as shown in the figure below:

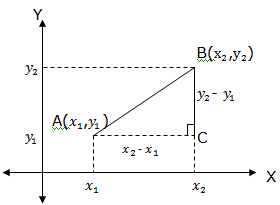
The distance between A and B in terms of x₁, y_1,x₂, and y₂can be found as follows:Join AB and draw doted lines as shown in the figure above.

Then, AC = x₂– x₁and BC = y₂– y₁

Since the triangle ABC is a right angled, then by applying Pythagoras theorem to the triangle ABC we obtain

Therefore the distance is 13 units.

Parallel and Perpendicular Lines

Gradients in order to Determine the Conditions for any Two Lines to be Parallel

Compute gradients in order to determine the conditions for any two lines to be parallel

The two lines which never meet when produced infinitely are called parallel lines. See figure below:

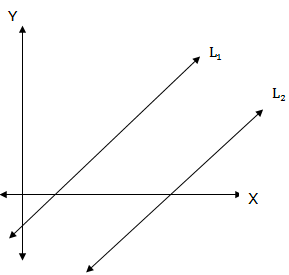
The two parallel lines must have the same slope. That is, if M₁is the slope for L₁and M₂is the slope for L₂thenM₁= M₂

Gradients in order to Determine the Conditions for any Two Lines to be Perpendicular

Compute gradients in order to determine the conditions for any two lines to be perpendicular

When two straight lines intersect at right angle, we say that the lines are perpendicular lines. See an illustration below.

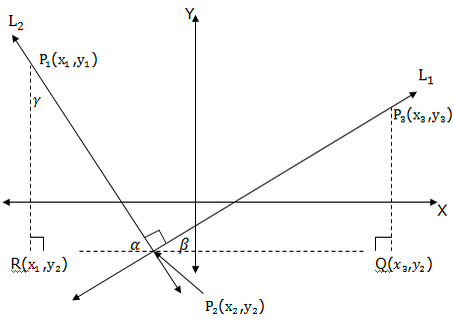
Consider the points P₁(x₁,y₁), P₂(x₂,y₂), P₃(x₃,y₃), R(x₁,y₂) and Q(x₃,y₂) and the anglesα,β,γ(alpha, beta and gamma respectively).

• α+β = 90 (complementary angles)
• α+γ= 90 (complementary angles)
• β = γ (alternate interior angles)

Therefore the triangle P₂QP₃is similar to triangle P₁RP_2.

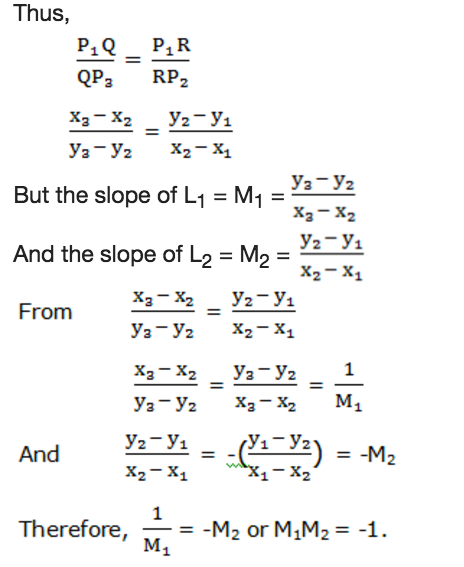
Generally two perpendicular lines L₁and L₂with slopes M₁and M₂respectively the product of their slopes is equal to negative one. That is M₁M₂= -1.

Example 10

Show that A(-3,1), B(1,2), C(0,-1) and D(-4,-2) are vertices of a parallelogram.

Solution

Let us find the slope of the lines AB, DC, AD and BC

We see that each two opposite sides of the parallelogram have equal slope. This means that the two opposite sides are parallel to each other, which is the distinctive feature of the parallelogram. Therefore the given vertices are the vertices of a parallelogram.

Problems on Parallel and Perpendicular Lines

Solve problems on parallel and perpendicular lines

Example 11

Show that A(-3,2), B(5,6) and C(7,2) are vertices of a right angled triangle.

Solution

Right angled triangle has two sides that are perpendicular, they form 90°.We know that the slope of the line is given by: slope = change in y/change in x

Now,

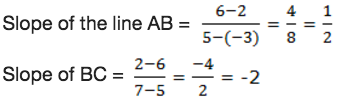
Since the slope of AB and BC are negative reciprocals, then the triangle ABC is a right angled triangle at B.

• READ TOPIC 2: Area And Perimeter

...