PHYSICS FORM ONE TOPIC 3: MEASUREMENT

MEASUREMENT

Concepts of Measurement

The Concepts of Measurement

Explain the concepts of measurement

Measurement is the process of assigning numbers to observations or events.

Importance of Measurement in Real Life

State the importance of measurement in real life

Measurements are so often taken for granted, we sometimes do not appreciate the grand importance measurements play in our lives. On a baseline level, measurements fall into the categories of weight, area, volume, length and even temperature. While we look at these various categories as stoic forms of mathematical measurements, a closer examination of things we do in everyday life reveals their clear importance.

Taking proper medicine. If you are ill (whether a serious or minor illness) you need to take your medicine and take it in the proper amount. If you take too little or too much then you are not going to get the proper benefit from it.

Cooking properly. Cooking of all forms is based on proper attention to measurement. Can you bake a chicken at 600 degrees? Well, you can but the results would be pretty catastrophic! Could you may a cup of tea by dipping a tea bag into a teaspoon of warm water?

Purchasing clothes. Now, how important could measurements be when selecting clothes? After all, to look good in clothing the main thing you need to pay attention to is style, right? Well, if you weigh 200lbs you aren't going to look stylish in an extra small shirt. Clothing is all based on size and proper fitting which are, of course, variants of measurement.

Playing sports. The importance of measurements may not necessarily reveal itself when you play sports but it is there in a big way. If you want to throw a runner out at first or make a 30 yard touchdown pass then you really need to be accurate and comes from a clear sense of depth and distance.

Making estimations. If you have to be at school at 9am what time would you have to leave in the morning if you are at your friend's house. Often we do not have an exact answer so we need to make an estimation which is essentially a guess of measurement.

Keeping yourself warm or cool. If the temperature outside dips or increases you have to make an adjustment on your thermostat in order to remain at a safe and healthy temperature. Understanding the measurement scale of a thermostat is critical in this regard or else you may find yourself feeling rather uncomfortable.

Understanding weight. Is that object too heavy to pick up by yourself or do you need to use something to lift it? Some may think this is not important but it is pretty easy to hurt yourself if you lift objects that are too heavy.

Proper use of capacity. Just how many clothes can you fit in a dresser or closet without it becoming too crammed? Without a clear concept of capacity you might find yourself pouring an entire half gallon of orange juice into a small glass!

Telling time. The ability to tell time is all based on measurement principles. Whether you are using a digital clock or an hourglass these devices measure the passage of time. Now, imagine how chaotic the world would be if if was impossible to measure the passage of time.

Transportation. How much weight is too much for a plane to take off or a car to move efficiently? How much fuel is needed to reach a certain point and how long will it take to get somewhere? Yes, measurements play a significant part in transportation.

Structure. This was saved for last because it is the common theme that is found in all the multitude of reasons for the importance of measurements. Measurements provide structure and remove the chaos that would result without any congruent method of understanding weight, mass, temperature, etc.

Basic Fundamental Quantities

A Fundamental Quantity

Define a fundamental quantity

Physical quantity:Is any character which can be measured by an instrument.

A Unitis the standard which is used to explain measurement of a body.Eg; kilogram, metre, second etc.

Fundamental quantitiesare numbers that we need to describe the world around us, which we cannot express in terms of "simpler," more basicquantities. Here is an example: My weight is not afundamental quantity, because it depends on how much stuff makes up my body.

Three Basic Fundamental Quantities of Measurement

Mention three basic fundamental quantities of measurement

Basic fundamental quantitiesare physical quantities from which other physical quantities are derived from. This includes three quantities namely mass, length and time.

The S.I Unit of Fundamental Quantity

State the S.I unit of fundamental quantities

SI unit (International system of units): Is the system of units which is used internationally to measure three basic physical quantities.

SI units of fundamental quantities

Basic physical quantity	SI unit
Mass	Kilogram (kg)
Length	Meter (m)
Time	Second(s

Metric system

Is an international system which is a decimal based system, consequently, conversions from one unit to another within the metric system can accomplished by multiplying or dividing by ten or power of ten.

Note: With the exception of temperature, amount of substance and luminous intensity international other units of measurement that are smaller or larger than the most commonly used units are expressed by attaching a prefix to the most commonly used units.

More than 1 unit

• Giga(G) = 1,000,000,000 (10ˆ9)
• Mega(M) = 1,000,000 (10ˆ6)
• Kilo(K) = 1,000(10ˆ3)
• Hector (h) = 100(10ˆ2)
• Decca(da) = 10(10ˆ1)1

Less than 1 unit

• Deci (d) = 1/10 (10ˆ-1)
• Cent (c) = 1/100(10ˆ-2)
• Mill (m) = 1/1000 (10ˆ-3)
• Micro(μ) = 1/1,000,000(10ˆ-6)

Appropriate Instruments for Measuring Fundamental Quantities

Use appropriate instruments for measuring fundamental quantities

Length, l

Length is the distance between two points, objects or space.The SI unit of length is meter(m). Other commonly used units are kilometer(km) and centimeter(cm).

1km = 1000m

1m = 100cm

The instrument used to measure length is the metre rule.

How to read the metre rule:Owing to the thickness of the wood,the eye must always be placed vertically above the mark being read, in order to avoid errors due to parallax.

Measuring of length (diameter) of small objects.

The diameter of small objects is measured by using two instruments:

1. Vernier caliper
2. Micrometer screw gauge

A venier caliper is the instrument used to measure length to the accuracy of 0.01cm.It is used to measure lengths to the range of 1.0cm to about 12.0cm.The figure below describe the structure of vernier caliper.

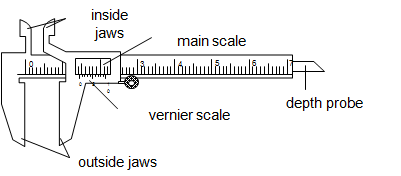
The main scale is graduated in centimeter (cm) while the vernier scale is graduated in millimeter (mm).The vernier scale is a short scale 9mm long divided into 10 equal parts, so that the difference in length between a vernier division and the main scale division is 0.1mm or 0.01cm.

The inside jaws are used to measure the inside diameter while the outside jaws are used to measure outside diameter.The vernier slides over the main scale.

How to read

• The main scale reading is recorded. This is the reading which precedes the zero mark of the vernier scale.
• The vernier scale reading is recorded by reading the mark on it which coincide with a mark on the main scale (i.e. vernier scale reading x 0.01cm).
• The summation of these two readings is the length of the object measured.

A micrometer screw gauge:Is an instrument used to measure length to the accuracy of 0.001cm(0.01mm).It is used to measure the diameters of wires and ball bearings. It can measure small lengths up to about 2.5cm.The diagram below describes the micrometer screw gauge.

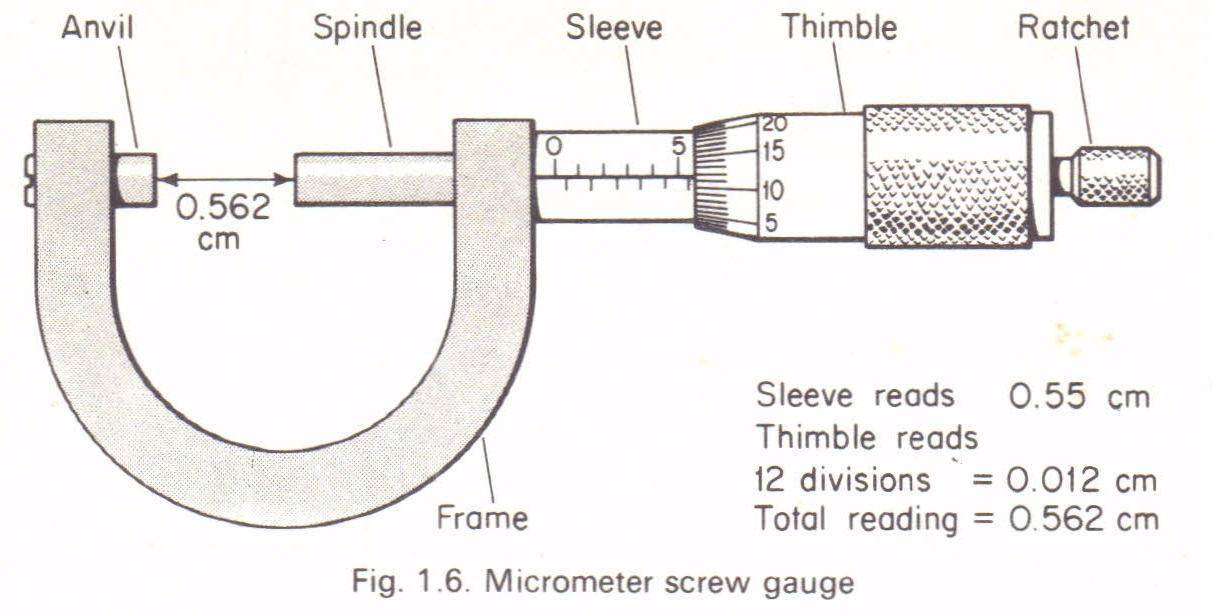
It consists of a spindle which is fitted with a graduated thimble. The screwed portion of a spindle is totally enclosed to protect it from damage.The pitch of the screw is 0.5mm, so that the spindle moves through o.o5cm for each complete turn.

The anvil and the spindle grip the measured object between them. The ratchet prevents the user from using undue pressure. The sleeve is graduated in mm, each graduation represent one complete turn of the screw.

How to read a micrometer screw gauge:

• Sleeve reading is recorded. This gives the units and the first two decimal places in mm.
• Thimble reading is then recorded. This gives the third decimal place (thimble reading x 0.001mm).
• The summation of these two readings gives the diameter of the object under measurement.

Precautions when using a micrometer screw gauge.

1. Before use,the faces of anvil and spindle should be wiped clean to remove any dirty particle which would give false readings.
2. Check and record for zero error then + or –the correction to the final answer.

Mass

Mass of a body is the amount of matter it contains. The SI unit of mass is kilogram(kg). Other commonly used units are gram(g) and tones(t).

1kg = 1000g

1t = 1000kg

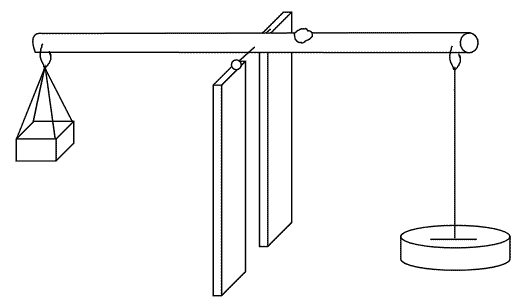
The mass of a body doesn’t change from place to place. The instrument used to measure mass is called abeam balance.

Difference between mass and weight:

Mass	Weight
Is the amount of matter contained	Is the force by which the earth pull a body to its centre
SI unit is kilogram	SI unit is Newton
Doesn’t vary from place to place on the earth’s surface	Varies from place to place on the earth’s surface
Measured by beam balance	Measured by a spring balance

Time

Is the gap between two occasions or events.The SI unit of time second(s). Other units used are minutes (min), hour(h),day etc.

1min = 60s

1h = 3600s

1day = 86400s

The instruments for measuring time are clocks and watches.

Derived quantities

Derived Quantities

Explain derived quantities

Derived quantities are units which are derived from the fundamental quantities. Examples are volume, density, power, work, energy, weight, frequency etc.

The S.I Units of Derived Quantities

State the S.I. units of derived quantities

SI units of Derived quantities

Volume	Cubic meter (mˆ3)
Density	Kg/mˆ3
Power	Watts (W)
Work	Joules (J)
Energy	Joules (J)
Weight	Newton (N)
Frequency	Hertz (Hz)

Basic Apparatus/equipment's and their uses

Basic Apparatus/Equipments Used for Measurement

Describe basic apparatus/equipments used for measurement

Volume

Volume is the amount of space occupied by a substance. The SI unit is cubic meter (mˆ3).Other units used are cubic centimetre (cmˆ3) and litre(l).

Instruments used to measure the volume of liquids:

Measuring cylinder-used for measuring or pouring out various liquids.

Measuring flask and pipette are used for getting fixed pre-determined volume.

Flask

Pipette

Burette-used to deliver any required volume up to its total capacity.

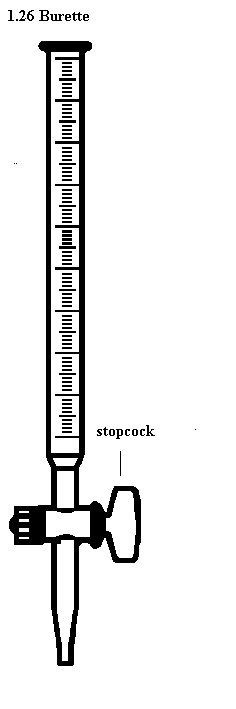
How to read volume measuring instruments(precautions).

Readings are always taken at the level of the bottom of the meniscus or curved surface of the liquid. Mercury is an exception as its meniscus curves downwards.

Care should be taken to place the eye correctly to avoid parallax errors. When taking readings, the pipette and burette must be upright and the cylinder and flask must stand on a horizontal bench otherwise errors may arise from tilting.

Measuring volume of irregular objects.

The volume of an irregular solid can be determined by measuring the volume of water displaced in a measuring cylinder directly or with the aid of an overflow eureka can.

Activity 1

Experiment

Aim: To measure the volume of an irregular object.

Methods

By using a measuring cylinder directly

Materials and apparatus: Irregular object eg; stone, thread, measuring cylinder, eureka can and water.

Procedures

• Poor a known volume of water in a burette(V1)
• Tie a stone with a thread.
• Immerse the tied stone in water holding the thread and record the volume (V2)
• Make sure the stone is totally immersed in water.

Results

• Volume before introducing solid = V1
• Volume after introducing solid = V2
• Volume of irregular solid(V3) = V2 – V1

By using the eureka can

Procedureto follow:

• Poor water into eureka can up to its spout
• Immerse a well tied stone in water completely
• Collect the overflowed water in the water.
• Use a measuring cylinder to determine the volume of water collected

Observation

• When a stone was introduced in an overflow can, water overflowed to the measuring cylinder.
• The volume of water collected is equal to the volume of irregular object(stone)

Sources of Errors in Measurement

Identify sources of errors in measurement

Error is the difference between the measured value and the real or actual value (The difference in reading is known as the error).

There are two types of errors, namely:

1. Systematic errors
2. Random errors

Systematic errors

Systematic errors results in the measurement or reading being consistently over the actual value OR consistently smaller than the actual value.

Sources of systematic errors.

1. Zero error: Zero Error is caused if the reading shown is Not zero when the true value is actually zero. This is most probably caused by a flaw in the instrument for example when using a ruler that has lost its zero scale due to wear and tear hence causing an error in the measurement of length.
2. Wrong assumptions: For example if you assume that water boils at 100 degree Celsius but actually its boiling point is higher if there are impurities in it. (Pure water boils at 100 degree Celsius).
3. Lag of reaction time: For example in a sports day, when measuring a 100 m running time using a stopwatch. The observer may not press the stop button exactly when the foot of the runner touches the finishing line.
4. Calibration errors: Instruments that are not properly calibrated could also cause error and this has to be put in consideration when writing a report or when there is an anomaly in reading.

Random errors.

Random error is caused by the observer who reads the measuring instrument. Just like the systematic error, there is also positive or negative error. Positive error is when the reading is bigger than the real value and negative error is when the reading is smaller than the real value.

Ways of reducing errors

1. Taking several readings and then find the average.
2. Avoiding parallax error by positioning the instrument (meter rule) properly on the table with the eyes perpendicular to the scale.
3. Some instruments can be adjusted to eliminate zero error. For example when using an ammeter, there is an adjuster to set the indicator to zero before making any measurement.
4. In the case of a ruler, measurement can be carried out starting from the next clear scale for example if scale 0.0cm is blurred, we can start measuring the length from 2.0cm, of course taking the difference of value in consideration when recording the final reading.

Density and Relative Density

The Concept of Density of a Substance and its S.I Unit

Explain the concept of density of a substance and its S.I unit

The Density of a substance is its mass per unit volume.

The unit of density is kg/mˆ3. Other unit used is g/cmˆ3.Density of regular solid object can easily be found by direct and easy measurements.-It involves measuring the mass and calculating the volume as described in the experiment below.

The Density of Regular and Irregular Solids

Determine the density of regular and irregular solids

Activity 2

Experiment

Aim;To measure the density of rectangular block.

Material and Apparatus :Ruler, beam balance and rectangular block.

Procedures:Using a beam balance measure mass of the block, m.Measure its length, width and height.

Results

• The mass of the rectangular block is m.
• The volume of the rectangular block will be calculated by multiplying the obtained length, l height, h and width, w.
• Volume, V = l x h x w, But; Density = mass/volume
• The volume of a material can be obtained by using various methods depending on the shape of the material

Activity 3

Experiment.

Aim; To determine density of irregular solid.

Materials and apparatus:Irregular solid like stone, measuring cylinder, beam balance and water.

Procedures

• Obtain the mass of the given object using the beam balance.
• Fill water to the measuring cylinder to the volume V₁.
• Immerse the well tied irregular object totally in the cylinder containing water.
• Record the new volume V₂.

Results

• Volume of irregular object = V₂ - V₁
• Mass obtained = M

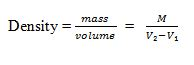
The Density of a Liquid

Determine the density of a liquid

Density of liquids can be determined by using a burrete or a density.

Activity 4

Experiment.

Aim: To determine density of liquids using a burette.

Materials and apparatus: Burette, beaker, beam balance and kerosene.

Procedures

• Record the mass of the empty beaker m₁ using a beam balance.
• Pour the known volume of kerosene into the beaker by using bur rete, V.
• Record the mass of the beaker and kerosene m₂.

Results

Definition of the Relative Density of a Substance

Define the relative density of a substance

The Relative density of a substance is the ratio of its density to the density of water.The density of water has the density of approximately 1.0g/cm³ or 1000kg/m³.

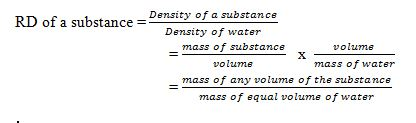
Note:Since the density of pure water is 1g/cm³, the RD of a substance will be represented by the same number as its density in g/cm³.RD has no units as its ratio of same quantities.

Applications of Density and Relative Density in Real Life

Interpret applications of density and relative density in real life

Application of RD in real life.

1. It is the key factor which is considered during the design of various structures and equipment. Eg. ships and planes.
2. Density is considered during the selection of materials.
3. Density is also considered during the design of equipment used in swimming.

• READ TOPIC 4: Force

...