PHYSICS FORM ONE TOPIC 8: WORK, ENERGY AND POWER

WORK, ENERGY AND POWER

Work

The Concept of Work

Explain the concept of work

If a person pushes a wall and the wall does not move, though the person may sweat and physically become tired, he would not have done any work. But if the person pushes a trolley and the trolley moves it is said work is done.

The S.I Unit of Work

State the S.I unit of work

Work is the product of force and distance moved in the direction of the force.

Thus,

Work = Force (f) * distance (d) moved in the direction of the force.

SI unit of work is Joules.

The Work Done by an Applied Force

Determine the work done by an applied force

Example 1

A sack of maize, which weighs 800N, is lifted to a height of 2m. What is work done against gravity?

Data given:

Force (f) = 800N

Height distance = 2m

Work done = ?

Solution:

Work done (w.d) = force (f) x distance (d)

w.d = 800N x 2m

= 1600 Joules

Work done (w.d) = 1600Joules

Energy

The Concept of Energy

Explain the concept of energy

Energy can be defined as capacity of doing work.

Energy has the same SI unit like that of work, and that is Joules (J)

S.I Unit of Energy

State S.I unit of energy

Energy has the same SI unit like that of work, and that is Joules (J)

Different Forms of Energy

Identify different forms of energy

There are different forms of energy such as:

1. Chemical energy
2. Heat energy
3. Light energy
4. Sound energy
5. Electrical energy
6. Nuclear energy
7. Solar energy

Difference between Potential Energy and Kinetic Energy

Distinguish between potential energy and kinetic energy

There are two types of chemical energy, which are:

1. Potential energy:It is the energy possessed by a body mass in its position or state.
2. Kinetic energy: It is the energy possessed by a body due to its motion.

Consider when the body is vertically thrown upwards with an initial velocity ‘u’ from the ground.

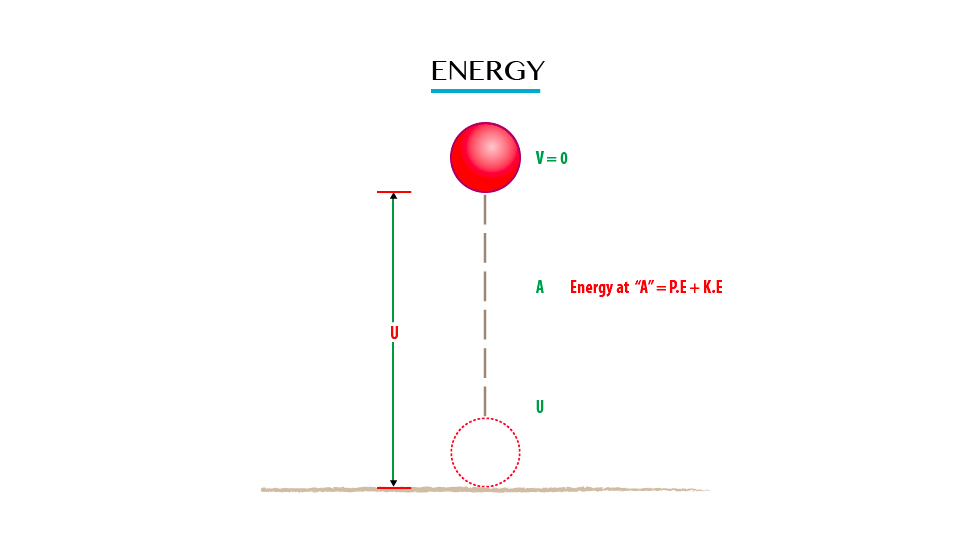
At the ground:The height is zero and initial velocity is at maximum so as to attain maximum height.

Therefore K.E = ½ MV² will be maximum

K.E_max = ½ mv²

Where K.E = Kinetic energy

M = Mass of the object/body

V=Velvety

P.E = Mgh

Where

P.E = Potential energy

M= Mass of the object

H = Height of the object

g = gravitation force

P.E = Mgh will be zero because P.E

= M*g*0 (body at the ground where k=0)

Neglecting the air resistance, as the body moves upwards its velocity decreases it also experiences gravitational force (g) pulling downwards towards the earth’s centre.

The maximum Height Attained

The final velocity of the body will be zero (V=0)

Therefore K.E = ½ mv²

K.E = ½ m(0)²

K.E = 0

P.E = MgHmax

Note:That the object drops from Hmax that is; it leaves with zero Kinetic Energy. At position A in fig. 8. The conservation of mechanical energy (M.E) is given as:

P.E + K.E = Constant

(The sum of P.E and K.E is constant throughout the motion of the object if the air resistance is neglected)

The Transformation of Energy

Explain the transformation of energy

The notion of energy is that energy is changed from one form into different forms using transducers.

Transducer is a device used to transform energy from one form to another.

For example:

1. Battery converts chemical energy into electrical energy.
2. A generator converts mechanical energy into electrical energy.
3. A motor converts electrical energy into mechanical energy.

The Table Summarising Energy Transformation

ORIGINAL ENERGY	TRANSDUCER	ENERGY TRANSFORMED
Chemical energy	Battery	Electrical energy
Chemical energy	Motor	Chemical energy
Mechanical energy	Generator	Electrical energy
Solar energy	Solar panel	Electrical energy
Chemical energy	Motor car	Mechanical energy
Electrical energy	Microphone	Sound energy
Electrical energy	Heater	Heat energy

Activity 1

To demonstrate pressure of potential energy.

Materials and Apparatus

1. A heavy stone
2. A bucket full of water
3. A strong inelastic rope; and
4. Smooth pulley

Procedures:

• Collect the heavy stone, using a strong rope tie it to a bucket of water
• Pass the rope over smooth pulley fixed to a support.
• Hold stationary the heavy stone at height “h” above the ground
• Release the stone

Results and observations:

• When the stone released the bucket of water will start to rise.
• The stone is said to have potentials energy because of its position above the ground.
• Lifting a body of mass “m” to a height “h” above the ground requires work to be done against gravity. Work = Mgh

Example 2

A ball of mass 0.5 kg is kicked vertically upwards and rises to a height of 5m. Find the potential energy by the ball.

Data given:

Mass of the ball (Mb) = 0.5 kg

Height (h) = 5m

Gravitation force (g) 10N/kg

Potential energy (P.E) = ?

Solution:

Potential energy (P.E)= mgh

= 0.5kg x 10N/kg x 5m

= 25 NM

1NM= 1Joules

Potential energy (P.E) = 25 Joules.

Activity 2

Aim: to investigate the law of conservation of energy by a simple pendulum.

Materials and Apparatus:A pendulum bob and light inelastic string.

Producers

• Pull the bob of a simple pendulum in position A so that it is at height “h” above position B.
• Release the bob so that it swings to position C via the lowest position B and back to A.
• Consider the figure below:

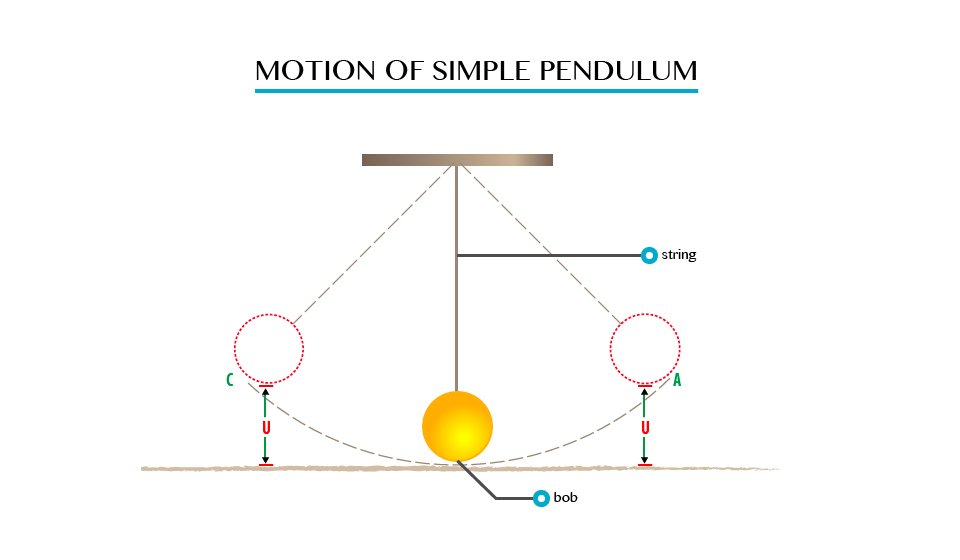
Observation

When the bob is at position A, it possesses potential energy only due to the height “h” which is equal to “Mgh”.

As it swings downwards to position B, the height decreases, and as the result it loses potential energy.

• The bob has Vmax and hence K.Emax at B. The height at B is zero, thus the P.E is zero.
• As it swings towards C, the P.E increases and reaches its maximum again in position C, where the Kinetic Energy is zero. At position D, the energy of the bob is party potential and party Kinetic.

The Principle of Conservation of Energy

State the principle of conservation of Energy

The law of conservation of energy state that “ Energy can neither be created nor destroyed but can only be converted from one form to another.”

This means the amount of energy is constant all the time.

Example 3

A stone of mass 2kg is released form a height of 2m above the ground. Find the potential energy of the stone when it is at the height of 0.5m above the ground.

Data given;

Mass of the stone (Ms) = 2kg

Height released (h) = 2m

Gravity (g) = 10N/kg

Potential energy = (P.E) ?

Solution:

P.E at height g 2m

P.E = Mgh

= 21g x 10N/kg x 2m

P.E = 40 Joules

P.E at 2m = 40Joules

Than P.E at height of 0.5m

= 21g x 10N/kg x 0.5m

P.E at 0.5m = 10Joules

100s of P.E = 40 Joules - 10Joules

= 30 Joules

According to conservation of energy the loss of P.E should be equal to the gain in K.E, when the air resistance is neglected.

K.E of the stone at 0.5 above the ground = 30 Joules

Example 4

A ball of mass 0.21kg is dropped from a height of 20m. on impact with the ground it loses 30J of energy. Calculate the height which it reaches on the rebound.

Data given;

Mass of ball (Mb) = 0.2kg

Height dropped (h) = 20m

Loose in energy (E) 30J

Height which reaches=?

Solution;

Consider the figure below;

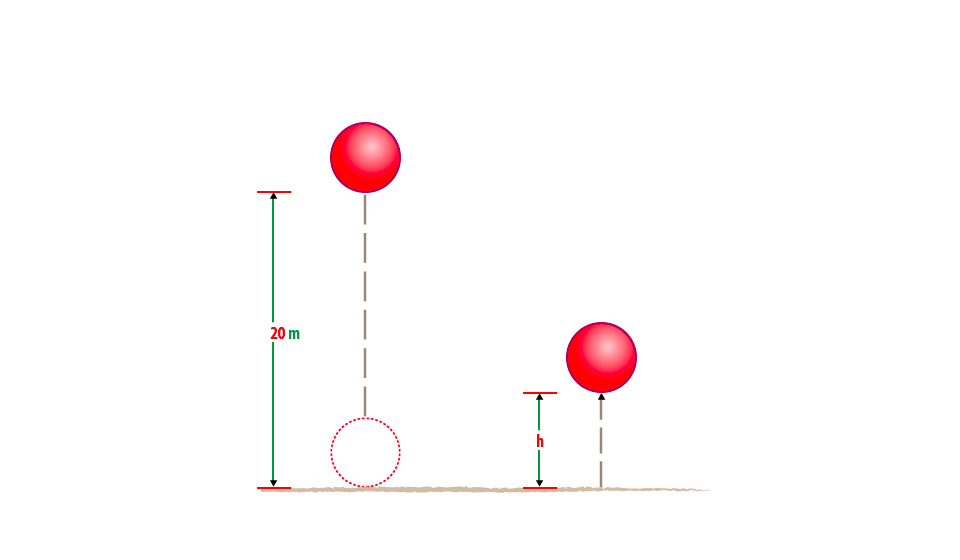
At 20m above ground the initial energy of the ball = Mgh

= 0.2kg x 10N/kg x 20m

= 40 Joules.

So after the impact the ball loose 30J and the energy remaining is 40 J-10J

= 10Joules

At the top of rebound the energy of the ball = potential energy (P.E)

The height reaches (h) is 5m.

Uses of Mechanical Energy

Explain the uses of mechanical energy

The mechanical energy can be used to produce electric power using generators. Some uses of mechanical energy are: It enables our body to do work, it makes work easier and faster, it is used to transport goods and people from one place to another, many transport vehicles uses the knowledge of mechanical energy. Examples of vehicles which uses mechanical energy are airplanes and motor cars.

Power

The Concept of Power

Explain the concept of power

Power is the rate of which work is done.

• It is a measure of the rate at which energy changes.
• This means that whenever work is done energy changes into a different form.

The S.I Unit of Power

State the S.I unit of power

The SI unit of power is Jules per second J/S or watts, W.

1 Joules per second = 1 watt

When 1 Joules of work is done per second the power produced is a watt. Watt is the unit for measuring electrical power.

The Rate of Doing Work

Determine the rate of doing work

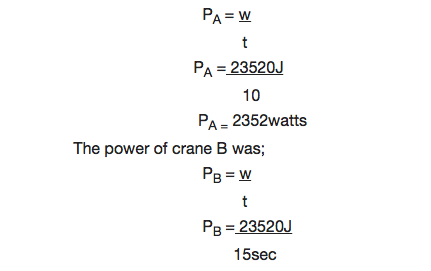
Suppose that two cranes each lift objects having masses of 200kg to a height of 12m. Crane A lifts its object in 10sec while crane B requires 15sec to lift its object. Assume they lift the objects at a constant velocity they do the same amount of work.

Work done = GPE

= Mgh

= (200kg) (9.8m/s²⁾(12m)

= 23520J

Each did a work that was equivalent to 23520J.

What is different for the two cranes is the rate at which they did the work or their generation of power.

The power of crane A can be calculated by;

P_B = 1568 watts.

Example 5

How much power is required to accelerate a 1000kg car from rest to 26.7m/s in 8sec?

Solution:

The work done on the car increases its Kinetic energy.

Work done = AKE

½ MV² – ½ MV²

The power required is given by:

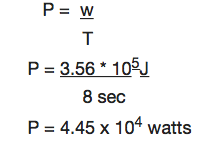
Example 6

Car engine is rated in horsepower (hp) where 1hp = 746watts. What is the required power measured in horsepower?

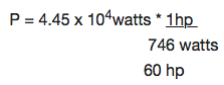
Since work causes a change in energy. DE power can be considered as the rate of change of energy.

P = DE/t

• READ TOPIC 9: Light

...