
MOTION IN STRAIGHT LINE
Motion is the change of position of an object from one place to another. There are two types of motions; i.Circular motion-Is the motion of an object in a circle. Examples; a/. motion of the electron around the nucleus of an atom b/.revolutionary movement of the earth around the sun. ii.Linear motion-Is the motion of an object in a straight line.
Distance and Displacement
Difference between Distance and Displacement
Distinguish between Distance and Displacement
Distance Is the length between two points or two objects.It is a scalar quantity i.e. it has a magnitude only but no direction. Its symbol is X or S and the SI unit is meter (m). Other units used are Kilometer (km) and Centimeter (cm)
Displacement Is the distance in a specific direction. It is a vector quantity i.e. it has both magnitude and direction.
Differences between distance and displacement
| Distance | Displacement |
| Is the length moved by an object between two points | Is the distance in a specific direction |
| It is a scalar quantity | It is a vector quantity |
The SI Units of Distance and Displacement
State the SI units of Distance and Displacement
The symbol for distance is X or S and the SI unit is meter (m). Other units used are Kilometer (km) and Centimeter (cm)
The standard unit of displacement in the International System of Units ( SI ) is the meter (m).
Speed and Velocity
Difference between Speed and Velocity
Distinguish between Speed and Velocity
Speed
Speed is the distance moved by an object in a unit time or is the rate of change of distance . It is a scalar quantity.
Velocity
Velocity is the displacement moved by an object per unit time or is the rate of change of displacement. It is a vector quantity and its symbol is U or V.
Formula for speed and velocity
Speed(velocity) = Distance/displacement x time taken
X = Vt
Note:36km/h = 10m/s
Differences between speed and velocity
| Speed | Velocity |
| Is the rate of change of distance | Is the rate of change of displacement |
| It is a scalar quantity | Is a vector quantity |
The SI Unit of Speed and Velocity
State the SI unit of Speed and Velocity
The SI unit of speed and velocity is meter per second (m/s). Other units are Km/h or cm/s
The Average Velocity of a Body
Determine average velocity of a body
Types of velocity
- Initial velocity, U – Is the velocity of a body at the start of observation
- Final velocity, V – is the velocity of a body at the end of observation
- Average velocity –is the average or mean between initial and final velocity or is the ratio of the total displacement to the total time.
- Uniform or constant velocity Is the one whereby the rate of change of displacement with time is constant.
- Absolute velocity is the actual velocity of a moving object recorded by a stationary observer
- Relative velocity is the velocity of a moving object recorded by a moving observer .
- Instantaneous velocity is the velocity of a moving object recorded at any time.
Acceleration
Acceleration is the rate of change of velocity or is the change in velocity per unit time Mathematically. Acceleration, a = (final velocity, v – initial velocity, u)/time, t
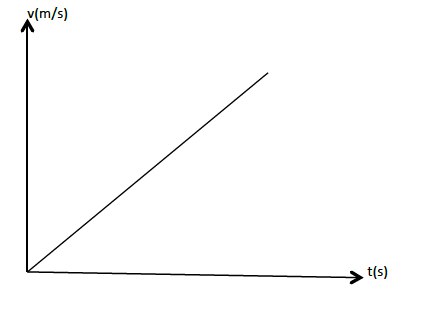
Velocity Time-graph
Interpret velocity time-graph
This is velocity against time graph. Consider a body accelerating uniformly from rest to a certain velocity v within time t. This can be represented graphically as shown below;
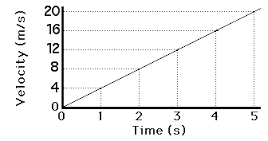
Distance
- The distance x moved by the body is given by the area under the curve.
- In this case is the area of triangle OBC.
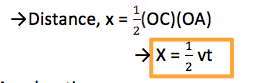
Acceleration.
- The acceleration is given by the slope of the triangle OBC.
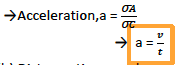
The Acceleration of a Body
Determine the acceleration of a body
Example 1
A car starts from rest and accelerates to a velocity of 120m/s in one minute. It then moves with this speed for 40seconds finally decelerates to rest after another 2 minutes. Calculate;
- the distance travelled
- the total time taken for the whole motion
- the deceleration
- the average velocity
Soln
1st stage; acceleration u =0, v = 120m/s,t1 =1min=60s
2nd stage; uniform vel u=v=120m/s,t2=40s
3rd stage; Deceleration u=120m/s,v=0,t3=2min=120s
- 1st stage; s =average vel x time = ( (120+0)/2)60 = 3600m
- 2nd stage; s = vt = 120 x 40 = 4800m
- 3rd stage; s = average vel x time = ((v=u)/2)t = ((120+0)/2)120 = 7200m
Total distance, s T =3600+4800+7200 =15600m
Total time taken = 60 + 40 + 120 = 220s
from v = u + at
120 = 0 + 60a
60a = 120
a = 2m/s.
Average velocity = total distance/time
va = 15600/220
va = 71m/s
The Concept of Retardation
Explain the concept of retardation
Deceleration (retardation) is the rate of decrease of velocity or is the decrease in velocity per unit time. Uniform acceleration or retardation Is the one whereby the rate of increase or decrease of velocity is constant or it doesn’t change.
Note;
- when a body starts from rest or is brought to rest, its velocity is zero
- when the velocity of a body is constant or uniform, its acceleration is zero
- when the velocity of a moving object increases, its acceleration becomes positive
- when the velocity of a moving object decreases, its acceleration becomes negative called retardation.
Equations of Uniformly Accelerated Motion
Equation of Uniformly Accelerated Motion
Derive equation of uniformly accelerated motion
There are three equations of motion;
Newton’s first equation of motion
It is given by; v = u + at
whereby;
- u = initial velocity
- v = final velocity
- a = acceleration
- t = time taken
PROOF;
From the formula of acceleration; a = (v-u)/t
- at = v – u at + u = v
- v = u + at proved!
Newton’s second equation of motion
It is given by
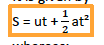
whereas;
- s=distance travelled
- u=initial velocity
- t=time taken
- a=acceleration
PROOF;
Suppose an object starts from rest with intial vel,u to final vel,v after time t The distance ,S moved is given by S = Average vel x time S =( (u+v)/2)t
Substitute Newtons first eqn,gives; S = ((u+u+at)/2)t
S = ((2u+at)/2)t
S = ut + 1/2at. proved!
Newtons third equation of motion
It is given by V2 = U2+ 2as
where v=final velocity; u =initial velocity; a = acceleration; s = distance covered.
PROOF
From Newton’s first eqn; v = u + at
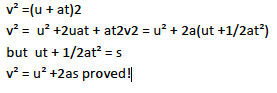
Equations of Accelerated Motion in Daily Life
Apply equations of accelerated motion in daily life
Activity 1
Apply equations of accelerated motion in daily life
Motion under Gravity
The Concept of Gravitational Force
Explain the concept of gravitational force
The acceleration of a free falling body is known as the acceleration due to gravity denoted by g and controlled gy gravitational force of the earth.
When two bodies of different masses are released from a certain height h above the ground, they will reach the ground at different times with the heavier one reaching earlier before the lighter one.
The reason is that the air resistance is more effective on lighter bodies than in heavier bodies, consequently this affect acceleration due to gravity in a reverse manner.
But dropping a light object and a heavy object in a vacuum they will reach the ground at the same time due to the absence of air resistance effect.
Consider the following two cases;
Case I
Consider a body falling freely from a certain height h and uses time t to reach the ground.
In this case: acceleration, a = acceleration due to gravity g
Initial velocity, u = 0
Final velocity, v.

Case II
Consider a body thrown vertically upwards from the ground with an initial velocity u to a certain height h and then comes back to the ground after time t.
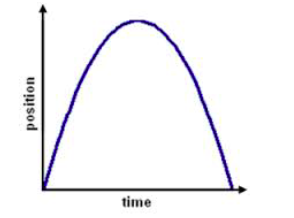
In this case;
- Acceleration, a = -g
- Initial velocity = u
- Velocity at h = 0
- Final velocity at the ground = v
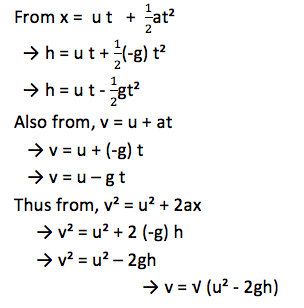
Acceleration due to Gravity
Determine acceleration due to gravity
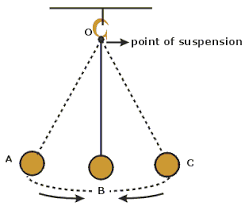
A simple pendulum is a small heavy body suspended by a light inextensible string from a fixed support and it is normally used to determine acceleration due to gravity.
It is made by attaching a a long thread to a spherical ball called a pendulum bob. The string is held at a fixed at a fixed support like two pieces of wood held by a clamp and stand.
If the bob is slightly displaced to position B,it swings to and from going to C through O and back to B through O. When the pendulum complete one cycle/revolution the time taken is called the period of oscillation, T.
Definitions
- Period ,T is the time taken by the pendulum bob to complete one complete cycle.
- Angular displacement is the angle made between the string and the vertical axis when the bob is displaced to a maximum displacement.
- Amplitude is the maximum displacement by which the pendulum has been displaced.
- Length of pendulum is the length of the string from the point of attachment on the wooden pieces to the canterof gravity of the bob.
From the experiments, it has been observed that, changing the weight of the bob and keeping the same length of pendulum, the period is always constant provided that all swings are small though they may be different in size.
The period T of the pendulum is given by;
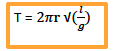
Where; l = length of pendulum; g = acceleration due to gravity
Also
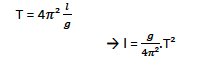
It follows that if we plot a graph of l against T. it is going to be a straight line with a slope g/4Π2and y –intercept equal to 0.
When the bob is raised to point B it will gain potential energy and the bob will swing due to the conservation of energy from potential to kinetic energy.
- At B and C all energy is P.E.
- At O all energy is K.E.
- P.E at B = K.E at O.
If the pendulum swung in vacuum the oscillations would have been continuous. But practically, air friction causes losses of energy of the pendulum bob. That is why after a certain time the oscillations cease.
The Application of Gravitational Force
Explain the application of gravitational force
Activity 2
Experiment
Aim: Determination of acceleration due to gravity by using the simple pendulum.
Materials and apparatus: A simple pendulum, stand, clamps and stop watch.
Procedures
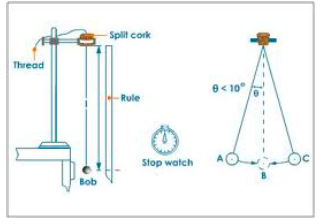
- Tie a piece of thread to a brass bob(about 100g)
- Suspend a bob with a thread between wooden pieces by clamping them on to a stand.
- Pull the bob slightly to one side and release the bob. Make sure the bob swings 50 complete oscillations.
- To be more accurate, perform three measurements for each length l of the pendulum.
- Repeat the procedures with l = 60cm and 50cm.
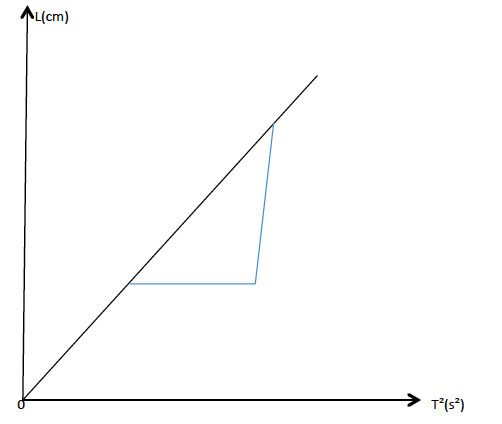
- Record the results as in the table below. -Plot the graph of l against T2
Results
| Length, l (cm) | Time for 50 oscillations. | T (s) | T² (s²) | |||
| t₁ (s) | t₂ (s) | t₃ (s) | Average(s) | |||
Observation
The graph obtained will be a straight line through the origin.
The slope of the graph is given by;
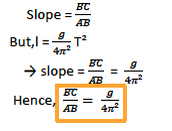
From this equation, the acceleration due to gravity can be computed easily.
- READ TOPIC 7: Newton's Law Of Motion



No comments:
Post a Comment