|
P
|
Q
|
R
|
(a)
|
(b)
|
(c)
|
Basic conjunction of (a)
|
Basic conjunction of (b)
|
Basic conjunction of ( c)
|
|
T
|
T
|
T
|
T
|
T
|
F
|
P ∧ Q ∧ R
|
P ∧ Q ∧ R
|
|
|
T
|
T
|
F
|
F
|
T
|
T
|
|
P ∧ Q ∧ ~ R
|
P ∧ Q ∧ ~ R
|
|
T
|
F
|
T
|
T
|
T
|
T
|
P ∧ ~ Q ∧ R
|
P ∧ ~ Q ∧ R
|
P ∧ ~ Q ∧ R
|
|
T
|
F
|
F
|
F
|
T
|
F
|
|
P ∧ ~Q ∧ ~ R
|
|
|
F
|
T
|
T
|
F
|
F
|
F
|
|
|
|
|
F
|
T
|
F
|
F
|
F
|
F
|
|
|
|
|
F
|
F
|
T
|
F
|
F
|
F
|
|
|
|
|
F
|
F
|
F
|
F
|
F
|
T
|
|
|
~ P ∧ ~ Q ∧ ~ R
|
→The required sentence for (a) is (P ∧ Q ∧ R) V (P ∧ ~ Q ∧ R)
→The required sentence for (b) is (P ∧ Q ∧ R) V (P ∧ Q ∧ ~R) V (P∧ ~Q ∧ R) V (P ∧ ~Q∧ ~ R)
→The required sentence for (c) is (P ∧ Q ∧ ~R) V (P ∧ ~Q ∧ R) V (~P ∧ ~Q ∧ ~R)
2. i) construct a truth table for ~ (P → Q)
ii) Write a compound sentence having that truth table (involving ~, ∧ , v)
3. Repeat for the following sentence
i) ~ P → ~Q ii) ~ p Q
More question
1. Find a compound sentence having components P and Q which is true and only if exactly one of its components P, Q is true.
2. Find a compound sentence having components P, Q and R which is true only if exactly two of P, Q and R are true.
3. Give an example of sentence having one component which is always true
4. Give an example of a compound sentence having one component which is always false
5. Use laws of algebra of propositions to simplify ~ (p V q) ∧ (~ p ∧ q)
6. Show that p q and ~ p v q are logically equivalent
7. If Apq p ∧ q and Np ~ p write the following without ~ and A
i) ~ (p ∧ q)
ii)~ (p ∧ ~q)
iii) ~ (~ p ∧ q)
iv) ~ (p ∧ ~ q)
QUESTIONS
1. Rewrite the following without using the conditional
i) If it is cold, he wears a hat
ii) If productivity increases, then wages rise
2. Determine the truth value of the following
i) 2 + 2 = 4 if and only if 3 + 6 = 9
ii) 2 + 2 = 4 if and only if 5 + 1 = 2
iii) 1 + 1 = 2 if and only if 3 + 2 = 8
iv) 1 + 2 = 5 if and only if 3 + 1 = 4
3. Prove by truth table
i) ~ (p q) ≡ p ~q
ii) ~ (p q) ≡ ~ p q
4. Prove the conditional distributes over conjunction i.e.
[p → (q ∧ r)] ≡ (p → q) ∧ (p → r)
5. Let p denote ‘’ it is cold’’ and let q denote ” it rains “. Write the following statement in symbolic form
i) It rains only if it is cold.
ii) A necessary condition for it to be cold is that it rains.
iii) A sufficient condition for it to be cold is that it rains
iv) It never rains when it is cold.
6. a) Write the inverse of the converse of the conditional
” If a quadrilateral is a square then it is a rectangle”
b) Write the inverse of the converse of the contra positive of
“If the diagonals of the rhombus are perpendicular then it is a square”
LOGICAL IMPLICATIONS
A proposition P is said to be logically imply a proposition Q if p → Q is a tautology
Example
Show that p logically implies p v q
Solution; Construct a truth table for p → (p v q)
|
P
|
q
|
P v q
|
P → (p v q)
|
|
T
|
T
|
T
|
T
|
|
T
|
F
|
T
|
T
|
|
F
|
T
|
T
|
T
|
|
F
|
F
|
F
|
T
|
Since column 4 is a tautology then p logically implies p v q
ARGUMENTS
An argument in logic is a declaration that a given set of proposition p1, p2, p3….pn called premises yields to another proposition Q called a conclusion such as argument is denoted by p1, p2….pn Q
Example of an argument
If I like mathematics, then I will study, either I study or I fail. But I failed therefore I do not like mathematics.
VALIDITY OF AN ARGUMENT
Validity of an argument is determined as follows
→An argument P1, P2, P3… Pn  Q is valid if Q is true whenever all the premises P1, P2, P3… Pn are true
Q is valid if Q is true whenever all the premises P1, P2, P3… Pn are true
→Validity of an argument is also determined if and only if the proposition (P1 ∧ P2 ∧ P3 ∧ ….. Pn) → Q is a tautology
Example
Prove whether the following argument is valid or not P, P → Q  Q
Q
Solution:
Draw a truth table for [P ∧ P → Q] → Q
|
P
|
Q
|
P → Q
|
P ∧ (p → Q)
|
P ∧ (p → Q) → Q
|
|
T
|
T
|
T
|
T
|
T
|
|
T
|
F
|
F
|
F
|
T
|
|
F
|
T
|
T
|
F
|
T
|
|
F
|
F
|
T
|
F
|
T
|
1. Since in row 1 the conclusion is true and all the premises are true then the argument is valid
2. Since column 5 is a tautology then the argument is valid
QUESTION
Use the truth table to show whether the given argument is valid or not
P → Q, Q → R P → R
Example
Symbolize the given argument and then test its validity
*If I like mathematics, then I will study, either I study or I fail. But I failed, therefore I do not like mathematics.
Solution.
The given argument is symbolized as follows
Let p ≡ I like mathematics
q ≡ I will study
r ≡ I fail
Then given argument is as follows
P → q, q v r, r, ~p
Testing the validity
[(p → q) ∧ (q ∧ r)∧ r] → ~p
|
P
|
Q
|
r
|
P → q
|
q v r
|
3 ∧ 4 ∧ 5
|
~ p
|
6 → 7
|
|
T
|
T
|
T
|
T
|
T
|
T
|
F
|
F
|
|
T
|
T
|
F
|
T
|
T
|
F
|
F
|
T
|
|
T
|
F
|
T
|
F
|
T
|
F
|
F
|
T
|
|
T
|
F
|
F
|
F
|
F
|
F
|
F
|
T
|
|
F
|
T
|
T
|
T
|
T
|
T
|
T
|
T
|
|
F
|
T
|
F
|
T
|
T
|
F
|
T
|
T
|
|
F
|
F
|
T
|
T
|
T
|
T
|
T
|
T
|
|
F
|
F
|
F
|
T
|
F
|
F
|
T
|
T
|
Since column 8 is not a tautology the given argument is not valid
QUESTIONS
1. Translate the following arguments in symbolic form and then test its validity
i) If London is not in Denmark, then Paris is not in France. But Paris is in France, therefore London is in Denmark
ii) If I work I cannot study. Either I work or I pass mathematics. I passed mathematics therefore I studied.
iii) If I buy books, I lose money. I bought books, therefore I lost money
2. Determine the validity of
i) p → q, ~q ~p
ii)~p → q, p ~q
iii) [p → ~ q], r → q, r ~p
ELECTRICAL NETWORK
Electrical network is an arrangement of worse and switches that
will accomplish a particular task e.g. lighting a lamp, turning a
motor, etc
The figure below shows an electrical network
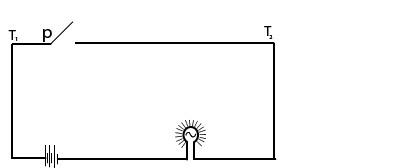
When the switch p is closed the current flows between T1 and T2
The above network simplifies to the following network

Relationship between statement in logic and network

A SERIES AND PARALLEL CONNECTION OF SWITCHES
A series connection of switches
The following switches are connected in series
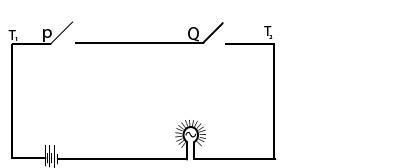
The current flow between T1 and T2 when both switches are closed current flows when p ∧ Q is true
A parallel connection of switches

The current will flow when either one of the switches is closed.
Currents flow when P V Q is true
Example
Consider the electrical network below

i) Construct a compound statement presenting the network above
ii) Find possible switch setting that will allow the current to flow between T1 and T2
Solution
Note i) current flows between T1 and T2 when switch p is closed i.e. p is true OR
ii) The current flows between T1 and T2 when switch switches q and r are closed i.e. Q ∧ R is true.
The required compound statement is p v (Q ∧ R)
iii) To find possible switch setting, draw a truth table P v (Q ∧ R)
|
P
|
Q
|
R
|
Q ∧ R
|
P V (Q ∧ R)
|
Current flows yes or No
|
|
T
|
T
|
T
|
T
|
T
|
Yes
|
|
T
|
T
|
F
|
F
|
T
|
Yes
|
|
T
|
F
|
T
|
F
|
T
|
Yes
|
|
T
|
F
|
F
|
F
|
T
|
Yes
|
|
F
|
T
|
T
|
T
|
T
|
Yes
|
|
F
|
T
|
F
|
F
|
F
|
No
|
|
F
|
F
|
T
|
F
|
F
|
No
|
|
F
|
F
|
F
|
F
|
F
|
No
|
Possible switch setting
|
P
|
Q
|
r
|
|
Closed
|
Closed
|
Closed
|
|
Closed
|
Closed
|
Closed
|
|
Closed
|
Closed
|
Closed
|
|
Closed
|
Closed
|
Closed
|
|
Closed
|
Closed
|
Closed
|
Questions
1. Construct compound statement that correspond to the networks
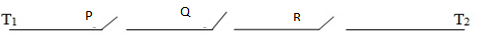
Solution
The current will flow when all three switches p, q, and r are closed i.e. p ∧ q ∧ r
The required compound statement is P ∧ Q ∧ R
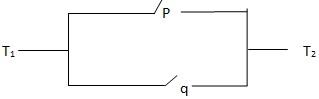
The required component statement is (P ∨ q)
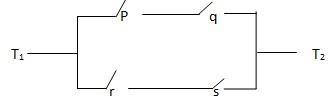
The required compound statement is (p ∧ q) V (r∧ s)

The required compound statement is P V Q V R

The required compound statement is p ∧ (q V (r ∧ s))
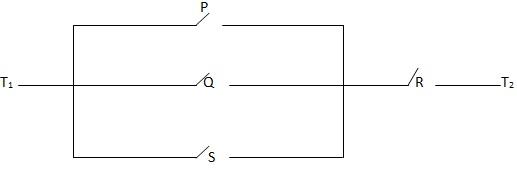
The required compound statement is (P ∨ Q ∨ R) ∧ S
2. In electrical network of (ii) find possible switch setting that will allow the current to flow between T1 and T2
ii) (P ∨ Q) ∧ R
|
P
|
Q
|
R
|
P V Q
|
(P V Q) ∧ R
|
|
T
|
T
|
T
|
T
|
T
|
|
T
|
T
|
F
|
T
|
F
|
|
T
|
F
|
T
|
T
|
T
|
|
T
|
F
|
F
|
T
|
F
|
|
F
|
T
|
T
|
T
|
T
|
|
F
|
T
|
F
|
T
|
F
|
|
F
|
F
|
T
|
F
|
F
|
|
F
|
F
|
F
|
F
|
F
|
Possible switch settings
|
P
|
Q
|
R
|
|
Closed
|
Closed
|
Closed
|
|
Closed
|
Open
|
closed
|
From statements to network
Example
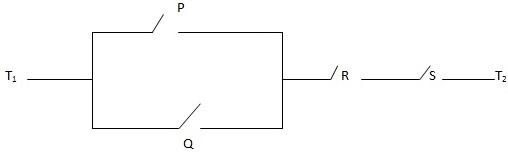
Draw a network for the statement (p v Q) ∧ (R ∧ S)
Solutions
Corresponding network is shown below
Questions
Draw network for the following statements
1. [P ∨Q ∧ (R ∧ S)]
2. [(P ∧ Q) ∧ (R V S)]
3. [P V (Q ∧ S) V (R ∧ T)]
4. (Q V(R V S) V P)
5. [P V (Q ∧ (R ∧ S)]
COMPLEX SWITCHES
These operates as follows
i) When one switch is closed, the other one closes also
ii) When one switch is closed, the other one opens
Refers to the diagram
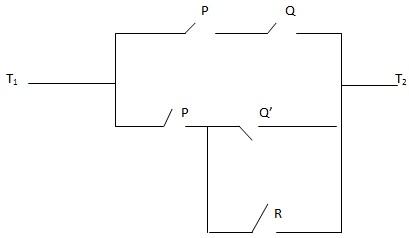
The compound relating to flow of electrical current is given
(P ∧ Q) V [P ∧ (~ Q V R)]
To find possible switch setting that will allow the current to flow between T1 and T2
– Draw a truth table for (P ∧ Q) V [ P ∧ ( ~ Q V R)]
1 2 3 4 5 6 7 8
|
P
|
Q
|
R
|
P ∧ Q
|
~ Q
|
~ Q V R
|
P ∧ (~ Q V R)
|
4 V 7
|
|
T
|
T
|
T
|
T
|
F
|
T
|
T
|
T
|
|
T
|
T
|
F
|
T
|
F
|
F
|
F
|
T
|
|
T
|
F
|
T
|
F
|
T
|
T
|
T
|
T
|
|
T
|
F
|
F
|
F
|
T
|
T
|
T
|
T
|
|
F
|
T
|
T
|
F
|
T
|
F
|
F
|
F
|
|
F
|
T
|
F
|
F
|
F
|
F
|
F
|
F
|
|
F
|
F
|
T
|
F
|
T
|
T
|
F
|
F
|
|
F
|
F
|
F
|
F
|
T
|
T
|
F
|
F
|
Possible switch setting
|
P
|
Q
|
R
|
|
Closed
|
Closed
|
Closed
|
|
Closed
|
Closed
|
Open
|
|
Closed
|
Open
|
Closed
|
|
Closed
|
Open
|
open
|
Example
Without using a truth table draw a sample network for the statement
(P ∧ Q) V [ P ∧ (~ Q V R)]
Solution
(P ∧ Q) V [ P ∧ (~ Q V R) ] = P ∧ (Q V (~ Q V R) ….. distributive
= P ∧ (Q V ~ Q) V R ……. associative
= P ∧ (t V R) ….. Complement
= P ∧ t ….. Identity
= P ….. Identity
The statement simplifies to p
The corresponding network is a follows

For a statement which on simplifying ends upon F network drawn is as follows

For a statement which upon simplifying yields to T, network is drawn as follows
 QUESTION
QUESTION
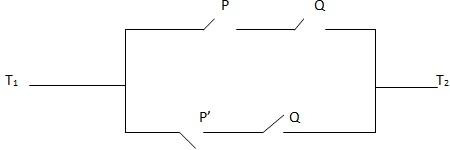
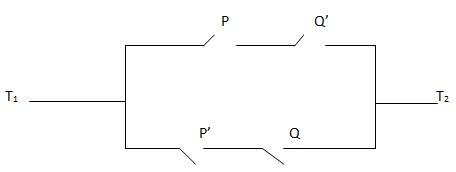
1. For each of the network shown below. Find a compound statement that represents it

2. (a) Draw network for the corresponding statement
i) (P ∧ ~ Q) ∨ (Q ∧ P)
ii) (P ∧ ~ Q) ∨(Q ∧ ~ R)
iii) P → Q ≡ ~ P ∨ Q
iv) (P → Q) ∧ (p v Q) ≡ (~ P V Q) ∧ (P V Q)
(b) Simplify the statement in 2 (iv) using the laws of algebra of propositions and draw a simple network
MORE QUESTIONS
i) Write down compound statement for the following networks
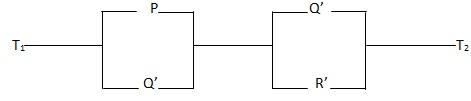
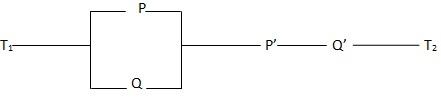
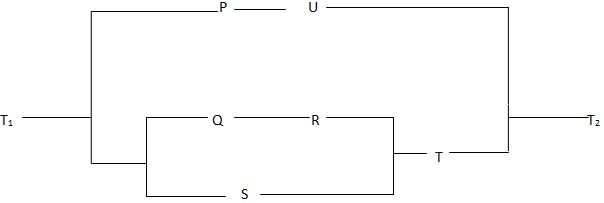
2. For each of these sentences draw a simple network
a) P∧ (~ Q → ~p)
b) ~ (P ∨ Q) →R
c) P ∧ ~ P
3. Given a truth table
|
P
|
Q
|
R
|
–
|
|
T
|
T
|
T
|
F
|
|
T
|
T
|
F
|
T
|
|
T
|
F
|
T
|
T
|
|
T
|
F
|
F
|
F
|
|
F
|
T
|
T
|
T
|
|
F
|
T
|
F
|
F
|
|
F
|
F
|
T
|
F
|
|
F
|
F
|
F
|
T
|
a) Construct a statement having this truth table
b) Draw the electrical network
Mathematics (from Ancient Greek μάθημα;
máthēma: ‘knowledge, study, learning’) is an area of knowledge that
includes such topics as numbers (arithmetic, number theory), formulas
and related structures (algebra), shapes and the spaces in which they
are contained (geometry), and quantities and their changes (calculus and
analysis).
Most mathematical activity involves the use of pure reason to
discover or prove the properties of abstract objects, which consist of
either abstractions from nature or—in modern mathematics—entities that
are stipulated with certain properties, called axioms. A mathematical
proof consists of a succession of applications of some deductive rules
to already known results, including previously proved theorems, axioms
and (in case of abstraction from nature) some basic properties that are
considered as true starting points of the theory under consideration.
Mathematics is used in science for modeling phenomena, which then
allows predictions to be made from experimental laws. The independence
of mathematical truth from any experimentation implies that the accuracy
of such predictions depends only on the adequacy of the model.
Inaccurate predictions, rather than being caused by incorrect
mathematics, imply the need to change the mathematical model used. For
example, the perihelion precession of Mercury could only be explained
after the emergence of Einstein’s general relativity, which replaced
Newton’s law of gravitation as a better mathematical model.
But for more post and free books from our site please make sure you
subscribe to our site and if you need a copy of our notes as how it is
in our site contact us any time we sell them in low cost in form of PDF
or WORD.
...
Thanks for reading MATHEMATICS FORM FIVE TOPIC 3: LOGIC (II)



No comments:
Post a Comment